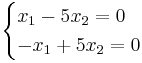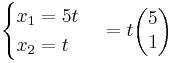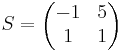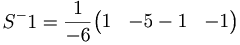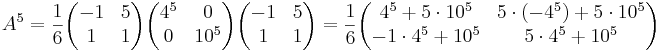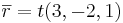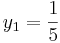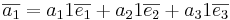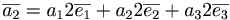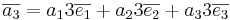MA1106/Lectures

From FUKTwiki

Revision as of 01:21, 24 May 2008 by Teddy (Talk | contribs)

(diff) ←Older revision | Current revision (diff) | Newer revision→ (diff)

Jump to: navigation, search

Student-made lectures notes in Linear Algebra (MA1106), in Swedish. Accuracy is not guaranteed!

[edit] Första föreläsningen

[edit] Linjär Algebra

Matrisberäkning
Skärningspunkter
Rumvridning

En linjär ekvation består av $a x + b y + c z + d = 0$ och kan även skrivas som $a 1 x 1 + a 2 x 2 + a 3 x 3 + d = 0$ .

Liknade ekvation som:

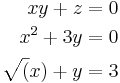
$\begin{align} xy + z = 0 \\ x^2 + 3y = 0 \\ \sqrt(x) + y = 3 \end{align}$

[edit] Gausseliminering

$\begin{cases} x_1 + 2x_2 + x_3 = 1 & \cdot [-3] \\ 2x_1 + 3x_2 - 2x_3 = 1 \\ 3x_1 + 4x_2 - 4x_3 = 1 \end{cases} \to \begin{align} -3x_1 - 6x_2 - 3x_3 = -3 \\ \underline{3x_1 + 4x_2 - 4x_3 = 1} \\ -2x_2 - 7x_3 = -2 \end{align}$

$\leftrightarrow$

$\begin{cases} x_1 + 2x_2 + x_3 = 1 & [\cdot (-2)] \\ 2x_1 + 3x_2 - 2x_3 = 1 \\ -2x_2 - 7x_3 = -2 \end{cases} \to \begin{align} -2x_1 - 4x_2 - 2x_3 = -2 \\ \underline{2x_1 + 3x_2 -2x_3 = 1} \\ -x_2 -4x_3 = -1 \end{align}$

$\leftrightarrow$

$\begin{cases} x_1 +2x_2 +x_3 = 1 \\ -x_2 -4x_3 = -1 & \cdot [-2] \\ -2x_2 -7x_3 = -2 \end{cases} \to \begin{align} 2x_2 + 8x_3 = 2 \\ \underline{-2x_2 - 7x_3 = -2} \\ x_3 = 0 \end{align}$

$\leftrightarrow$

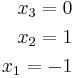
$\begin{align} x_3 = 0 \\ x_2 = 1 \\ x_1 = -1 \end{align}$

Linjära ekvationer kan ha tre typer av lösningar:

Oändliga
entydiga
saknad (inga)

[edit] Vanligt förekommande tentaliknande uppgift

EX: För alla värden av A och B, vilka har en entydig, oändlig eller saknad lösning?

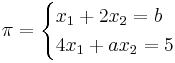
$\pi = \begin{cases} x_1 + 2x_2 = b \\ 4x_1 + ax_2 = 5 \end{cases}$

Svar:

$\begin{cases} x_1 + 2x_2 = b & \cdot [-4]\\ 4x_1 + ax_2 = 5 \end{cases} \to \begin{align} -4x_1 - 8_x2 = -4b \\ \underline{4x_1 + ax_2 = 5} \\ -8x_2 + ax_2 = 5 - 4b \end{align}$

Detta kan skrivas som $(a - 8) x 2 = 5 - 4 b$ och då är det möjligt att se vilka lösningar som a och b ger:

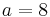$a = 8\,$	Oändligt antal lösningar
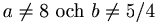$a \neq 8 \mbox{ och } b \neq 5/4\,$	entydiga lösning
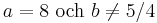$a = 8 \mbox{ och } b \neq 5/4\,$	saknar lösning

[edit] 2007-09-07

[edit] Allmänt

Skalär - Ett värde utan dimension (vanligt tal i motsatts till vektorer) 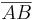$\overline{AB}$ - Riktad sträcka

En riktad sträcka bestäms av:

Riktning
Storlek
Startpunkt

En Vektor saknar startpunkt, och betecknas 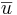$\overline{u}$ .

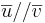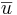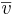$\overline{u}//\overline{v}$ betyder att $\overline{u}$ och $\overline{v}$ är parallella.

[edit] Vektormultiplikation

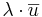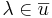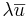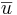För $\lambda \cdot \overline{u}$ så måste $\lambda \in \overline{u}$ och $\lambda \overline{u}$ vara parallell med $\overline{u}$ .

För den resulterade produktvektorn gäller:

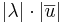Längden är $|\lambda| \cdot |\overline{u}|$ .
Riktningen förblir samma som 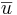$\overline{u}$ om $λ > 0$ .
Riktningen får motsatt riktning från 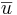$\overline{u}$ om $λ < 0$ .

[edit] Subtraktion mellan vektorer

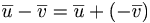
$\overline{u} - \overline{v} = \overline{u} + (-\overline{v})$

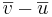
$\overline{u} - \overline{v}$ är parallell med $\overline{v} - \overline{u}$

[edit] Baser i planet, rummet och i en linje

I ett rum, plan eller linje måste alla baser vara ickeparallella med varandra.

Antal baser:

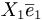
linjer = ska ha 1 basvektor. $X_1 \overline{e}_1$
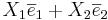
plan = ska ha 2 basvektorer. $X_1 \overline{e}_1 + X_2 \overline{e}_2$
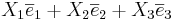
rum = ska ha 3 basvektorer. $X_1 \overline{e}_1 + X_2 \overline{e}_2 + X_3 \overline{e}_3$

Vektorer som är linjärt beroende med varandra kan ej utgöra mer än en bas.

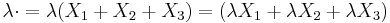
$\lambda \cdot = \lambda (X_1 + X_2 + X_3) = (\lambda X_1 + \lambda X_2 + \lambda X_3)$

$P :(X 1, X 2, X 3)$ är en punkt i rummet.

[edit] Linjärt beroende eller oberoende

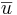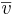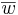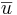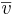Def: Ett antal vektorer kallas linjärt beroende om det finns reella tal som inte alla är lika med noll, så att: $\lambda_1 \overline{u}_1 \lambda_2 \overline{u}_2 \dots \lambda_k \overline{u}_k = 0$ , Annars så är vektorena linjärt oberoende. 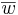Om $\overline{u}$ kan beskrivas med hjälp av vektorena $\overline{v}$ och/eller $\overline{w}$ så kan man kalla $\overline{u}$ en linjärkombination av $\overline{v}$ och/eller $\overline{w}$ .

Om man ställer upp vektorena i ett ekvationssystem, så gäller det att enbart om det finns en entydig lösning och den entydiga lösningen är $λ 1,λ 2,λ 3 = 0$ så kan man kalla att vektorena är linjärt oberoende.

Om $λ 1 = λ 2 = λ 3 = 0$ så kan man säga att vektorena är linjärt oberoende.

[edit] Example

a) $λ 1 (4,1, - 5) + λ 2 (2,1, - 1) + λ 3 (1,1,1) = 0$

$\begin{cases} 4 \lambda_1 + 2 \lambda_2 + \lambda_3 = 0 \\ \lambda_1 + \lambda_2 + \lambda_3 = 0 & \to [\cdot(5)] \to \\ -5 \lambda_1 + -\lambda_2 + \lambda_3 = 0 \end{cases} \begin{cases} 5 \lambda_1 + 5 \lambda_2 + 5 \lambda_3 = 0 \\ \underline{-5 \lambda_1 + -\lambda_2 + \lambda_3 = 0} \\ 4 \lambda_2 + 6 \lambda_3 = 0 \end{cases}$

$\begin{cases} 4 \lambda_1 + 2 \lambda_2 + \lambda_3 = 0 \\ \lambda_1 + \lambda_2 + \lambda_3 = 0 & \to [\cdot(-4)] \to \\ 4 \lambda_2 + 6 \lambda_3 = 0 \end{cases} \begin{cases} 4 \lambda_1 + 2 \lambda_2 + \lambda_3 = 0 \\ \underline{-4 \lambda_1 -4 \lambda_2 - 4 \lambda_3 = 0} \\ -2 \lambda_2 - 3 \lambda_3 = 0 \end{cases}$

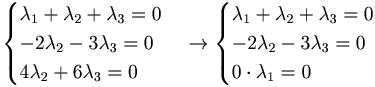
$\begin{cases} \lambda_1 + \lambda_2 + \lambda_3 = 0 \\ -2 \lambda_2 - 3 \lambda_3 = 0 \\ 4 \lambda_2 + 6 \lambda_3 = 0 \end{cases} \to \begin{cases} \lambda_1 + \lambda_2 + \lambda_3 = 0 \\ -2 \lambda_2 - 3 \lambda_3 = 0 \\ 0 \cdot \lambda_1 = 0 \end{cases}$

$λ 1 = t$
$λ 2 = t ( - 3)$
$λ 3 = 2 t$

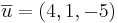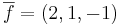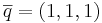Slutsats: $\overline{u} = (4,1,-5)$ har ett linjärt beroende med $\overline{f} = (2,1,-1)$ och $\overline{q} = (1,1,1)$ eftersom $λ 1$ , $λ 2$ och $λ 3$ inte är lika med 0.

[edit] 2007-09-12

[edit] Kap 3

Förkottningar:

R - reela tal
O - origo
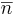$\overline{n}$ - Normalvektorn

[edit] 3.1 kordinatsystem

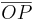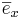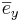
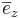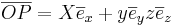Om man fixerar en punkt i O(origo) så kan läget av en godtycklig punkt P beskrivas med Vektorn $\overline{OP}$ . För en given bas $\overline{e}_x$ , $\overline{e}_y$ $\overline{e}_z$ finns då entydligt bestämda tal x,yz så att $\overline{OP} = X\overline{e}_x + y\overline{e}_y z\overline{e}_z$ .

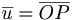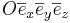Def! Vektorn $\overline{u} = \overline{OP}$ sägs vara ortsvektorn för punkten P. Talen x, y, z sägs vara kordinater för punkten P i kordinatsystemet $O\overline{e}_x\overline{e}_y\overline{e}_z$ .

Obs1! Koordinatsystemet behöver inte vara rätvinklikt.

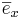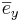
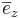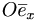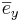
Obs2! Man använder baser $\overline{e}_x$ , $\overline{e}_y$ $\overline{e}_z$ för att representera vektorer. Man använder kordinatsystemet 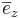$O\overline{e}_x$ , $\overline{e}_y$ $\overline{e}_z$ för att beskriva läget hos punkterna:

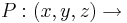$P:(x,y,z)\to$ Punkt
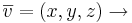$\overline{v}=(x,y,z)\to$ vektor

Obs3! Linjen genom O med riktningen 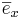$\overline{e}_x$ kallas för x-axel punkten :(1,0,0) kallas enhetspunkt längs x-axeln.

Planet genom O(origo) som innehåller x och y-axlarna kallas för xy-planet och skrivs Z=0. p.s.s Planet genom O som inehåller x och z kallas för xz-planet osv. Planen kallas gemensamt för koordinatplan.

Lemma: Låt $P 1 :(x 1, y 1, z 1)$ och $P 2 :(x 2, y 2$ då gäller 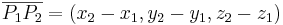$\overline{P_1P_2}=(x_2-x_1,y_2-y_1,z_2-z_1)$ .

EX: Ange kordinaterna för vektorena som går från $P 0$ :(1,3,4) till P:(2,0,5)

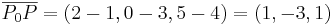$\overline{P_0P} = (2-1,0-3,5-4) = (1,-3,1)$ .
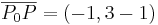$\overline{P_0P}=(-1,3-1)$ .

[edit] 3.2 Linjens Ekvation

En line är entydligt bestämd om man känner en punkt på linjen och vet att den är parallell med en vetkor 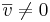$\overline{v} \neq 0$ . En godtycklig punkt P i rummet ligger på linjen om 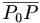$\overline{ P_0P}$ är parallell med 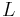$L\,$ (linjen) där $P 0$ ligger på linjen. 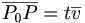$\overline{P_0P} = t\overline{v}$ för något tal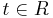 $t\in R$

Ex: I ett koordinatsystem i rummet finns punkten $P 0 :(x 0, y 0, z 0)$ och $P :(x, y, z)$ och en vektor 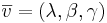$\overline{v}=(\lambda, \beta, \gamma)$ .
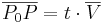$\overline{P_0P} = t \cdot \overline{V}$ där $t \in R$
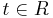
Detta kan skrivas som $(x - x 0, y - y 0, z - z 0) = (t λ, t β, t γ)$ .

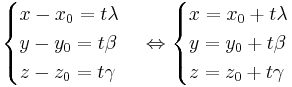
$\begin{cases} x-x_0 = t\lambda \\ y-y_0 = t\beta \\ z-z_0 = t\gamma \end{cases} \Leftrightarrow \begin{cases} x = x_0 + t\lambda \\ y = y_0 + t\beta \\ z = z_0 + t\gamma \end{cases}$

$x 0, y 0, z 0$ är en punkt på linjen.
$t λ, t β, t γ$ är linjens riktningsvektor.

EX: Ange en ekvation på paramerform för linjen genom punkterna (1,-1,4) och (2,3,5). Riktningsvektorn är ena punkten minus den andra

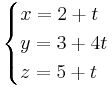
$\begin{cases} x=2 + t \\ y=3 + 4t \\ z=5 + t \end{cases}$

Ritningsvektorn 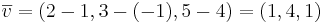$\overline{v}=(2-1,3-(-1),5-4) = (1,4,1)$

EX: Vad kan man säga om linjen l som har parameterformen.

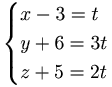
$\begin{cases} x - 3 = t \\ y + 6 = 3t \\ z + 5 = 2t \end{cases}$

Den går genom punkten (3,-6,-5) och har riktningsvetorn 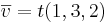$\overline{v} = t(1,3,2)$ .

EX: en linje har parameterformen:

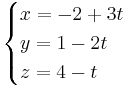
$\begin{cases} x = -2 + 3t \\ y = 1 - 2t \\ z = 4 - t \end{cases}$

a) ange en punkt på linjen

(-2,1,4)

b) ange en riktningsvektor för linjen

$\overline{r} = t (3,-2,1)$

c) hur får man andra punkter på linjen?

(1,-1,3)

d) finns det fler riktningsvektorer till linjen?

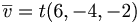$\overline{v} = t(6,-4,-2)$ , och dett finns oändligt antal av dom...

EX: Ange en linje som går genom punkten (1,3,1) och är parallell med linjen:

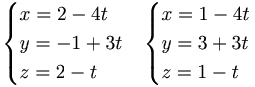
$\begin{cases} x = 2 - 4t \\ y = -1 + 3t \\ z = 2 -t \end{cases} \begin{cases} x = 1 - 4t \\ y = 3 + 3t \\ z = 1 - t \end{cases}$

EX: Skär linjerna varandra?

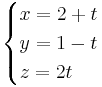
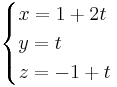
$\begin{cases} x = 2 + t \\ y = 1 - t \\ z = 2t \end{cases}$ $\begin{cases} x = 1 + 2t \\ y = t \\ z = -1 + t \end{cases}$

Om De skär varandra så har de en punkt gemensamt.

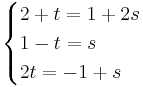
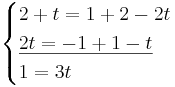
$\begin{cases} 2 + t = 1 + 2s \\ 1 -t = s \\ 2t = -1 +s \end{cases}$ $\begin{cases} 2 + t = 1 + 2 - 2t \\ \underline{2t = -1 + 1 -t} \\ 1 = 3t \end{cases}$

VL: $2 + 1 / 3 = 7 / 3$ HL: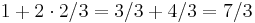 $1+2\cdot2/3=3/3+4/3=7/3$
VL: 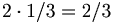$2\cdot1/3=2/3$ HL: $- 1 + 2 / 3 = - 3 / 3 + 2 / 3 = - 1 / 3$
Detta Stämmer EJ! Linjerna är inte parallella för att 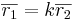$\overline{r_1}=k\overline{r_2}$ dvs
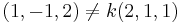
$(1,-1,2) \neq k(2,1,1)$

Linjer i planet:
EX: Bestäm en ekvation för linjen som går genom punkten (2,3) och som har riktningen (-1,3).
På Parameterform:

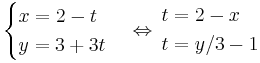
$\begin{cases} x = 2 -t \\ y = 3 +3t \end{cases} \Leftrightarrow \begin{align} t & = 2 - x \\ t & = y/3 -1 \\ \end{align}$
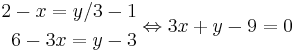
$\begin{align} 2-x = y/3 -1 \\ 6-3x=y-3 \end{align} \Leftrightarrow 3x + y -9 = 0$

$3 x + y - 9 = 0$ är skriven på affin form!

I planet finns alltså två sätt att skriva linjens ekvation. Dels i parameterfrom och dels i affin form.

EX: Skriv linjen $x - 2 y + 5 = 0$ i parameterform och ange dess riktningsvektor.

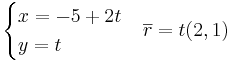
$\begin{cases} x = -5 + 2t\\ y = t \end{cases} \overline{r} = t(2,1)$

[edit] Sammanfattning om linjer

I rummet kan linjens ekvation skrivas på parameterform: 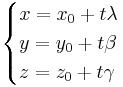$\begin{cases} x = x_0 + t\lambda \\ y = y_0 + t\beta \\ z = z_0 + t\gamma \end{cases}$ I planet kan lijens ekvation skrivas dels på paramterform och dels på affin form.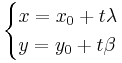 $\begin{cases} x = x_0 + t\lambda \\ y = y_0 + t\beta \end{cases}$
Där 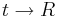$t \to R$ och $a x + b y + c = 0$ .

[edit] 3.3 Planets ekvation

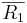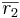Ett plan är entydigt bestämt om man känner en punkt $P 0$ och två vektorer $\overline{R_1}$ och $\overline{r_2}$ i planet och som inte är parallella. En godtycklig punkt P i rummet ligger i planet $π$ om och endast om 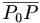$\overline{ P_0P}$ är parallell med planet 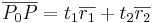$\overline{P_0P} = t_1 \overline{r_1} + t_2 \overline{r_2}$ för några tal $t 1$ och $t 2$ .

Obs! Om man inför ett kordinatsystem i rummet så behöver inte O(origo) ligga i plannet.

$P 0 :(x 0, y 0, z 0)$ $P :(x, y, z)$
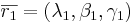
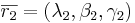
$\overline{r_1} = (\lambda_1, \beta_1, \gamma_1)$ $\overline{r_2} = (\lambda_2, \beta_2, \gamma_2)$
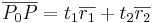
$\overline{P_0P} = t_1\overline{r_1} + t_2\overline{r_2}$
$(x - x 0, y - y 0, z - z 0) = t 1 (λ 1,β 1,γ 1) + t 2 (λ 2,β 2,γ 2)$

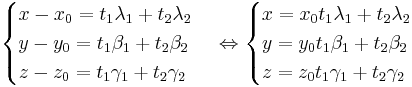
$\begin{cases} x - x_0 = t_1\lambda_1 + t_2 \lambda_2 \\ y - y_0 = t_1\beta_1 + t_2 \beta_2 \\ z - z_0 = t_1\gamma_1 + t_2 \gamma_2 \\ \end{cases} \Leftrightarrow \begin{cases} x = x_0 t_1\lambda_1 + t_2 \lambda_2 \\ y = y_0 t_1\beta_1 + t_2 \beta_2 \\ z = z_0 t_1\gamma_1 + t_2 \gamma_2 \\ \end{cases}$

$x 0, y 0, z 0$ är en punkt i planet $t 1 λ 1, t 1 β 1, t 1 γ 1$ är riktningsvektorn $t 2 λ 2, t 2 β 2, t 2 γ 2$ .

EX: Bestäm ekvationen för det plan som innehåller punkterna $(5,1,1,),(4, - 1,2),(2,2, - 3)$ .
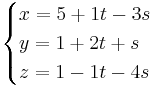
$\begin{cases} x = 5 + 1t -3s \\ y = 1 + 2t + s \\ z = 1 - 1t - 4s \end{cases}$

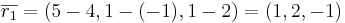
$\overline{r_1} = (5-4, 1 -(-1), 1-2) = (1,2,-1)$
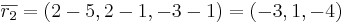
$\overline{r_2} = (2-5, 2-1, -3-1) = (-3,1,-4)$
På affin form blir det:
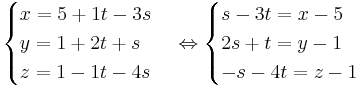
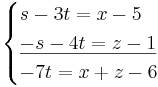
$\begin{cases} x = 5 + 1t -3s \\ y = 1 + 2t + s \\ z = 1 - 1t - 4s \end{cases} \Leftrightarrow \begin{cases} s - 3t = x -5 \\ 2s + t = y -1 \\ -s - 4t = z -1 \end{cases}$ $\begin{cases} s - 3t = x - 5 \\ \underline{-s -4t = z - 1} \\ -7t = x + z - 6 \end{cases}$
$\begin{cases} s-3t = x - 5 & [\cdot(-2)] \\ 2s + t = y - 1 \\ -7t = x + z -6 \end{cases} \begin{cases} -2s + 6t = 2x + 10 \\ \underline{2s + t = y -1} \\ 7t = -2x + y + 9 \end{cases} \Leftrightarrow \begin{cases} s - 3t = x -5 \\ 7t = -2x + y + 9 \\ -7t = x + z -6 \end{cases} \begin{align} & 7t = -2x + y +9 \\ & \underline{-7t = x + z - 6} \\ & 0 = -x + y + z + 3 \end{align}$

På affin form blir det då: $x - y - z - 3 = 0$ .

[edit] Klassiskt exempel

EX: Bestäm ekvariton för planet som går genom (1,0,0) (0,1,0) (0,0,1) på affin form.

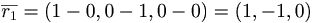
$\overline{r_1} = (1-0,0-1,0-0) = (1,-1,0)$
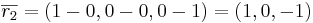
$\overline{r_2} = (1-0,0-0,0-1) = (1,0,-1)$

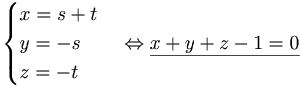
$\begin{cases} x = s + t \\ y = -s \\ z = -t \end{cases} \Leftrightarrow \underline{x + y +z -1 = 0}$

planets 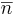$\overline{n}$ (normalvektorn) = (1,1,1)

Obs! $x + y + z - 1 = 0$ är parrallell med $x + y + z + 3 = 0$ , dvs alla $x + y + z + k = 0$ är parrallell med $c + y + z = 0$ .

[edit] Sats 2. Planets ekvation

Planets Ekvation kan skrivas del på parameterform:

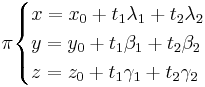
$\pi \begin{cases} x = x_0 + t_1\lambda_1 + t_2 \lambda_2 \\ y = y_0 + t_1\beta_1 + t_2 \beta_2 \\ z = z_0 + t_1\gamma_1 + t_2 \gamma_2 \end{cases}$

dels på Affin form $a x + b y + c z + d = 0$ där talen a,b,c inte alla är lika med noll.

Hur kommer man från affin form till parameterform?

EX: Skriv på parameterform ekvationen för planet $π: x + 4 y + 2 z - 8 = 0$

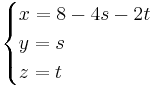
$\begin{cases} x = 8 - 4s - 2t \\ y = s \\ z = t \end{cases}$

tips: sätt y = s, z =t, och sätt in dessa i ekvationen för planet och lös ut f(x).

EX: Undersök om punkterna A:(1,0,0), B:(2,1,0) och C:(2,3,5) ligger i planet:

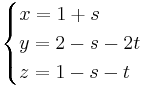
$\begin{cases} x = 1 + s \\ y = 2 - s - 2t \\ z = 1 -s -t \end{cases}$

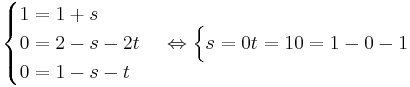
$\begin{cases} 1 = 1 + s \\ 0 = 2 -s -2t \\ 0 = 1 -s -t \end{cases} \Leftrightarrow \begin{cases} s = 0 t = 1 0 = 1 - 0 - 1 \end{cases}$

Med ovandnämnda metod så får man fram att:

A ligger i planet
B ligger i planet
C ligger inte i planet

Om ett plan skär kordinataxlarna i punkten (a,0,0), (0,b,0) och (0,0,c) så kan dess ekvation skrivas med interceptformlen $x / a + y / b + z / c = 1$ .

EX: Var skär planet $3 x + 6 y + 2 z - 6 = 0$ kordinataxlarna?

$3 x / 6 + 6 y / 6 + 2 z / 6 = 6 / 6$ dvs $x / 2 + y / 1 + z / 3 = 1$

[edit] 2007-09-14

Ex1: Var skär planet $2 x - 3 y + 5 z - 8 = 0$ kordinataxlarna?

$2 x / 8 - 3 y / 8 + 5 z / 8 = 8 / 8$

Planet skär x -axlen på $y = 4$

Planet skär y -axlen på $y = - 8 / 3$

Planet skär y -axlen på $y = 8 / 5$

Ex2: Bestäm skärningspunkten mellan planet $π:2 x - 3 y + z + 5 = 0$
Och linjen $L :(x, y, z) = (2,3, - 2) + t (2, - 1, - 4)$

beräkna linjens (x,y,z) kordinater först, dvs:

$((3 + 2 t),(5 - t),( - 2 - 4 t))$

Sätt in linjens kordinater $(x, y, z)$ i planets ekvation för att see var och om det finns en skärningspunkt.

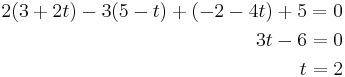
$\begin{align} 2(3 + 2t) - 3(5-t) + (-2-4t) + 5 = 0 \\ 3t - 6 = 0 \\ t=2 \end{align}$

Beräkna linjens kordinater för detta t, dvs:

Svar: Linjen skär planet i punkten $(7,3, - 10)$ .

[edit] Geometrisk teori för linjära ekvationsystem

$a x + b y + c z + d = 0$ är en ekvation för ett plan i rummet. Att lösa ett linjärt ekvationsystem innebär att man försöker finna gemensamma punkter för planen dvs. skärningspunkter.

Följande kan inträffa för planen!

(i)de saknar gemensamma punkter
(ii)de skär varandra i en punkt -entydig lösning
(iii)de skär varandra utefter en linje -oändligt antal lösningar
(iv)de är identiska

Har man endast två plan så kan inte (ii) inträffa.

Ex1: Bestäm skärningen mellan planet:

$π 1 : x - y + 3 z - 2 = 0$ och $π 2 :3 x + y + z - 6 = 0$

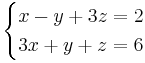
$\begin{cases} x - y + 3z = 2 \\ 3x + y + z = 6 \end{cases}$

Detta gör efter en viss beräkning att:

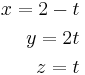
$\begin{align} x = 2 - t\\ y = 2t \\ z = t \\ \end{align}$

Om två plan är parallella eller identiska så gäller:

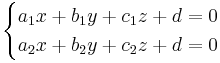
$\begin{cases} a_1x + b_1y + c_1z + d = 0 \\ a_2x + b_2y + c_2z + d = 0 \end{cases}$

Samtliga variablerna x,y,z försvinner om 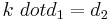$k \ dot d_1 = d_2$ .

Ex2: Avgör om vektorn $(7,4,16)$ är parallell med planet $π:4 x + y - 2 z + 1 = 0$ .
Ett plan parrallellt till $π$ men som går genom origo kan beskrivas som $π 1 :4 x - y - 2 z = 0$ .
Sätt in vektorn $(7,4,16)$ i detta plan så ger detta:

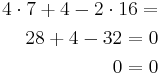
$\begin{align} 4 \cdot 7 + 4 - 2 \cdot 16 = \\ 28 + 4 - 32 = 0 \\ 0 = 0 \end{align}$

Alltså vetkorn är parallell med planet!

[edit] Kap4. Skalärprodukt

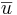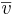4.1 Med den skalära produkten $\overline{u} \cdot \overline{v}$ av de två vektorerna $\overline{u}$ och $\overline{v}$ menas det reella talet:

$\overline{u} \cdot \overline{v} = \begin{align} |\overline{u}| \cdot |\overline{v}| \cdot \cos[\overline{u}, \overline{v}] \\ \mbox{0 om }\overline{u} \mbox{ eller }\overline{v} \mbox{ är = 0} \end{align}$

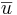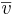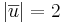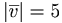Ex1: Beräkna skalärprodukten för vektorerna $\overline{u}$ och $\overline{v}$ med $|\overline{u}| = 2$ och $|\overline{v}| = 5$ om vinkeln melan dem är: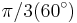 $\pi / 3 (60^\circ)$
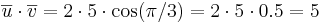
$\overline{u} \cdot \overline{v} = 2 \cdot 5 \cdot \cos (\pi / 3) = 2 \cdot 5 \cdot 0.5 = 5$

Arbete = 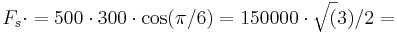$F_s \cdot = 500 \cdot 300 \cdot \cos (\pi/6) = 150000 \cdot \sqrt(3) / 2 =$

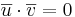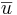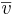Def: Om $\overline{u} \cdot \overline{v} = 0$ sägs $\overline{u}$ och $\overline{v}$ vara ortogonala(vinkelräta mot varandra) eftersom $cos(π / 2) = 0$

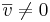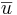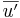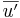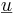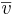Antag att $\overline{v} \neq 0$ för varje vetkor $\overline{u}$ definieras en vetkor $\overline{u'}$ . Vektorn $\overline{u'}$ kallas $\underline{u}$ :s ortogonala projektion på $\overline{v}$ .

[edit] Projektionsformlen

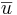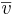Den ortogonala projektionen av $\overline{u}$ på $\overline{v}$ ges av formlen:

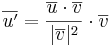
$\overline{u'}=\frac {\overline{u} \cdot \overline{v}} {|\overline{v}|^2} \cdot \overline{v}$

Sats2. Räknelagar för skalärprodukt.

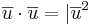
(i) $\overline{u} \cdot \overline{u} = |\overline{u}^2$
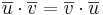
(ii) $\overline{u} \cdot \overline{v} = \overline{v} \cdot \overline{u}$
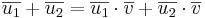
(iii) $\overline{u_1} + \overline{u_2} = \overline{u_1} \cdot \overline{v} + \overline{u_2} \cdot \overline{v}$
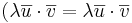
(iv) $(\lambda \overline{u} \cdot \overline{v} = \lambda \overline{u} \cdot \overline{v}$

[edit] 4.2 Ortonomerad bas

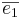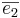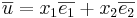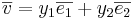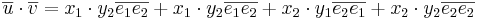
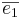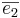För Koordinatuttrycket för skalärprdukt, låt $\overline{e_1}$ , $\overline{e_2}$ vara en bas i planet. om $\overline{u} = x_1 \overline{e_1} + x_2 \overline{e_2}$ och $\overline{v} = y_1 \overline{e_1} + y_2 \overline{e_2}$ så gäller enligt räknelagarna att $\overline{u} \cdot \overline{v} = x_1 \cdot y_2 \overline{e_1} \overline{e_2} + x_1 \cdot y_2 \overline{e_1} \overline{e_2} + x_2 \cdot y_1 \overline{e_2} \overline{e_1} + x_2 \cdot y_2 \overline{e_2} \overline{e_2}$

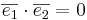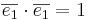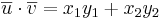Om $\overline{e_1}$ och $\overline{e_2}$ är ortogonala och har längden 1 dvs om $\overline{e_1} \cdot \overline{e_2} = 0$ och $\overline{e_1} \cdot \overline{e_1} = 1$ då blir skalärprodukten $\overline{u} \cdot \overline{v} = x_1y_1 + x_2y_2$ .

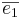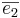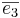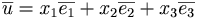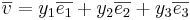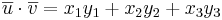Om $\overline{e_1}$ , $\overline{e_2}$ , $\overline{e_3}$ är en bas i rummet och $\overline{u} = x_1\overline{e_1} + x_2\overline{e_2} + x_3\overline{e_3}$ och $\overline{v} = y_1\overline{e_1} + y_2\overline{e_2} + y_3\overline{e_3}$ då blir $\overline{u} \cdot \overline{v} = x_1y_1 + x_2y_2 + x_3y_3$ under förutsättningen att 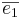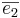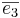$\overline{e_1}$ , $\overline{e_2}$ , $\overline{e_3}$ är ortonomerade om $\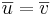overline{u} = \overline{v}$ .

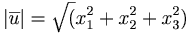$|\overline{u}| = \sqrt (x_1^2 + x_2^2 + x_3^2)$ dvs pytagoras sats

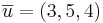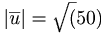
Ex1: om $\overline{u} = (3,5,4)$ så är $| \overline{u} | = \sqrt(50)$

Def. Vektorena 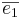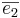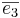$\overline{e_1}$ , $\overline{e_2}$ , $\overline{e_3}$ i rummet sägs utgöra en ortornomerad bas om de har längden 1 och att de är parvis vinkelräta. I tentorna så gäller det nästan alltid att uppgifterna har en ortornomerad bas

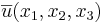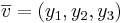Sats3 Om $\overline{u} (x_1, x_2, x_3)$ och $\overline{v} = (y_1, y_2, y_3)$ med avseende på en ortonomerad bas så är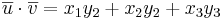 $\overline{u} \cdot \overline{v} = x_1y_2 + x_2y_2 + x_3y_3$

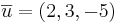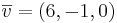Ex2 $\overline{u} = (2,3,-5)$ och $\overline{v} = (6,-1,0)$ i en ortonomerad bas.

a) beräkna skalärprodukten
- a = $\overline{u} \cdot \overline{v}$ vilket ger 9.
b) beräkna vinkeln mellan 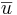och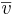
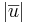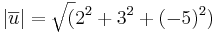- b = $\overline{u} \cdot \overline{v} = |\overline{u}| \cdot |\overline{v}| \cdot \cos[\overline{u},\overline{v}]$ . 9 är samma sak som $\overline{u} \cdot \overline{v}$ och $|\overline{u}|$ är roten ur total summan av varje kordinat uphöjt med 2, dvs $|\overline{u}| = \sqrt (2^2 + 3^2 + (-5)^2)$ .

Detta ger att b = 76°

basbyte vid ortonomerad bas
EX3: Låt 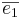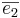$\overline{e_1}$ , $\overline{e_2}$ vara en ortonomerad bas i planet, visa att även:

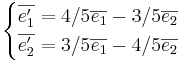
$\begin{cases} \overline{e_1'} = 4/5\overline{e_1} - 3/5\overline{e_2} \\ \overline{e_2'} = 3/5\overline{e_1} - 4/5\overline{e_2} \end{cases}$

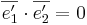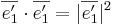Svar: Eftersom det är en ortonomerad bas så gäller det att $\overline{e_1'} \cdot \overline{e_2'} = 0$ . Med det så kan man beräkna. $\overline{e_1'} \cdot \overline{e_1'}= |\overline{e_1'}|^2$ . ............

4.3 Några geometriska Tillämpningar

Ex1: Två Vinkelräta komposanter varav den ena är parallell med vetkorn 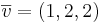$\overline{v} = (1,2,2)$ .

Projection formlen: 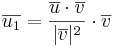$\overline{u_1} = \frac {\overline{u} \cdot \overline{v}} {|\overline{v}|^2} \cdot \overline{v}$

svar: (0,-1,1)

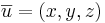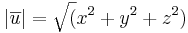
Avståndet mellan två punkter är absolut värdet av vektorn mellan punkterna. Absolut värdet av en vektorn kan beräknas med formlen $\overline{u} = (x,y,z)$ där $|\overline{u}| = \sqrt (x^2 + y^2 + z^2)$

Cirkelns ekvation i ett ekvationsystem:

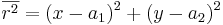
$\overline{r^2} = (x-a_1)^2 + (y-a_2)^2$

Sfär i rummets ekvation i ett ekvationsystem:

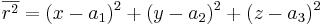
$\overline{r^2} = (x-a_1)^2 + (y-a_2)^2 + (z-a_3)^2$

[edit] Vinkelbestämning

Ex1: Bestäm vinkeln mellan linjerna:

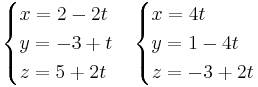
$\begin{cases} x = 2 - 2t \\ y = -3 + t \\ z = 5 + 2t \end{cases} \begin{cases} x = 4t \\ y = 1 -4t \\ z = -3 + 2t \end{cases}$

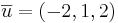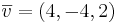Svar: två vektorer $\overline{u} = (-2,1,2)$ och $\overline{v} = (4,-4,2)$ . Skalärproduktformeln ger:

$\overline{u} \cdot \overline{v} = |\overline{u} \cdot \overline{v} \cdot \cos[\overline{u}, \underline{v}]$

$-4 = 9 \cos [\overline{u}, \overline{v}] = [\overline{u}, \overline{v}] = \arccos (-4/9) = 116^\circ$

[edit] Planets normalriktning

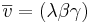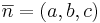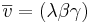Låt $π:(a x + b y + c z + d = 0)$ vara ett plan i rummet med vektorn $\overline{v} = (\lambda \beta \gamma)$ är parallell med planet om d i planets ekvation kan vara noll. men dår är $\overline{n} = (a,b,c)$ och $\overline{v} = (\lambda \beta \gamma)$ ortogonala. alltså skalärprodukten $(a, b, c)(λβγ) = 0$ om 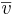$\overline{v}$ som är parrallell med planet är vinkelrät mot 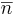$\overline{n}$ så måste 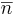$\overline{n}$ vara normal till planet.

Ex1: Planet $2 x + 3 y - 5 z + 7 = 0$ har normalvektorn 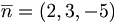$\overline{n} = (2,3,-5)$ .

Sats: För plan i rummet resp. linjer i planet gäller $a x + b y + c z + d = 0$ har normalen 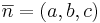$\overline{n} = (a,b,c)$ och linjen $a x + b y + c = 0$ har normalen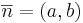 $\overline{n} = (a,b)$

Ex2: Bestäm vinkeln mellan planen $π 1 : x 1 + x 2 - 2 x 3 = 1$ och $π 2 : x 1 - x 3 = - 1$ .

Svar: Vinkeln mellan planen är samma som vinkeln mellan normal vektorena. dvs vinkeln mellan 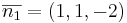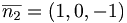$\overline{n_1} = (1,1,-2)$ $\overline{n_2} = (1,0,-1)$ . $(1,1,-2)(1,0,-1) = \sqrt(6) \cdot \sqrt(2) \cdot \cos[\overline{n_1},\overline{n_2}] = \arccos[\overline{n_1}, \overline{n_2}] = sqrt(3)/2$

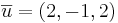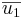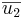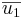Ex3: Låt $π$ vara planet $2 x - 4 y + 2 z = 0$ . Dela upp vektorn $\overline{u} = (2,-1,2)$ i vinkelräta komposanter $\overline{u_1}$ och $\overline{u_2}$ så att $\overline{u_1}$ är parrallell med planet och 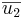$\overline{u_2}$ är vinkelrät mot planet.

svar: planets normal är 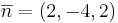$\overline{n} = (2,-4,2)$ skriven som $(1, - 2,1)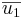$ . $\overline{u_1}$ säger vi är den vågräta vektorn och 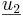$\underline{u_2}$ är den lodräta.

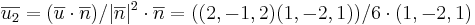
$\overline{u_2} = (\overline{u} \cdot \overline{n}) / |\overline{n}|^2 \cdot \overline{n} = ((2,-1,2)(1,-2,1))/6 \cdot (1,-2,1)$

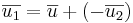
$\overline{u_1} = \overline{u} + (-\overline{u_2})$

[edit] 2007-09-19

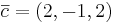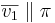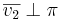EX: Låt $π$ vara planet $2 x - 4 y + 2 z = 0$ . Dela up vektorn $\overline{c} = (2,-1,2)$ i vinkelräta komposanter så att $\overline{v_1}\parallel\pi$ och $\overline{v_2} \perp \pi$ .

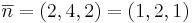
$\overline{n} = (2,4,2)=(1,2,1)$

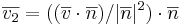
$\overline{v_2} = ((\overline{v} \cdot \overline{n}) / |\overline{n}|^2) \cdot \overline{n}$

$(((2, - 1,2)(1, - 2,1)) / 6)(1,2,1) = 6 / 6(1,2,1) = (1,2,1)$

$\overline{v_1} = \overline{v} - \overline{v_2} = (2,-1,2) - (1,2,1) = (1,-3,1)$

EX1: Spegla punkten P(2,3,4) i planet $π:(2 x + y - 2 z) = 0$ , ange koordinaterna för en speglade punkten.

Tips Origo finns i punkten eftersom det enkelt kan representeras av planets ekvation.

EX2: Spegla punkten P(2,3,4) i planet $π:(2 x + y - 2 z + 3) = 0$ , ange koordinaterna för en speglade punkten.

Tips Nu kan vi inte använda oss av Origo.
- Tips Skapa en punkt genom att sätta x,y till lämpligt värde (vanlig vis 0 eller 1) och räkna ut vad y ska bli.

$P :(2,3,4)$

$π:(2 x + y + 2 z + 3 = 0)$

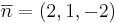
$\overline{n} = (2,1,-2)$

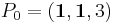
$P_0 = (\mathbf{1}, \mathbf{1}, 3)$

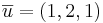
$\overline{u} = (1,2,1)$

Plan: Beräkna $u 1$ . Sedan ta två negativa $u 1$ och addera det med punkten vi vill spegla.

[edit] Avstånds formlen

Avståndet mellan punkter och plan/linje

$π: a x + b y + c z + d = 0$
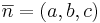
$\overline{n}=(a,b,c)$
$p 0 :(x 0, y 0, z 0)$
$A :(p, q, r)$
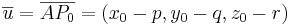
$\overline{u} = \overline{AP_0} = (x_0 - p, y_0 - q, z_0 - r)$
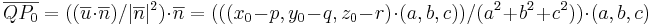
$\overline{QP_0} = ((\overline{u} \cdot \overline{n}) / |\overline{n}|^2) \cdot \overline{n} = (((x_0-p, y_0 - q, z_0 -r) \cdot (a,b,c)) / (a^2 + b^2 + c^2)) \cdot (a,b,c)$

Gör sammtliga utryck för 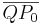$\overline{QP_0}$ i absolut form...

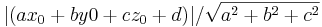$|(ax_0 + by0 + cz_0 +d)| / \sqrt{a^2 + b^2 + c^2}$ Detta är avstånds formlen!!!

avståndet mellan punkten $p 0$ och planet $π$ är 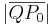$|\overline{QP_0}|$ .

EX: Ange avståndet från planet 3x - 4y + 12z = 13 till punkterna (0,0,0) och (2,1,3). Ligger punkterna på samma eller olika sidor om planet?

1. Punkten (0,0,0) i avståndsformlen:

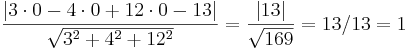
$\frac { | 3 \cdot 0 - 4 \cdot 0 + 12 \cdot 0 - 13 | }{ \sqrt {3^2 + 4^2 + 12^2} } = \frac { | 13 | } { \sqrt{169} } = 13/13 = 1$

2. Punkten (2,1,3) i avstånds formlen:

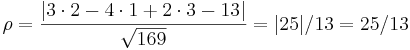
$\rho = \frac{|3 \cdot 2 - 4 \cdot 1 + 2 \cdot 3 - 13|}{ \sqrt{169}} = |25|/13 = 25/13$

Eftersom innan för absolut belopet är talen posetivt för det ena punkten, och negativ för den andra så ligger dom på olika sidor om planet!

EX: Bestäm den kortaste avståndet från punkten (1,2,3) till den räta linjen:

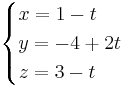
$\begin{cases} x = 1 -t \\ y = -4 + 2t \\ z = 3 -t \end{cases}$

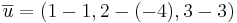
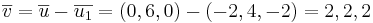
$A :(1, - 4,3)$ $\overline{u} = (1-1,2-(-4),3-3)$ $\overline{v} = \overline{u} - \overline{u_1} = (0,6,0) - (-2,4,-2) = 2,2,2$

Avståndet mellan punkterna och linjen är 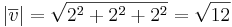$| \overline{v} | = \sqrt{2^2 + 2^2 + 2^2} = \sqrt{12}$

[edit] Kap 5

[edit] 5.1 Orientering

Def1: antag att de tre vektorena 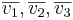$\overline{v_1}, \overline{v_2}, \overline{v_3}$ inte ligger i ett plan. Om den minsta vridning som överförs 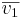$\overline{v_1}$ :s riktning i 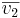$\overline{v_2}$ :s riktning ser ut att ske moturs från spetsen av 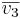$\overline{v_3}$ så sägs 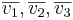$\overline{v_1},\overline{v_2},\overline{v_3}$ vara positivt orienterade.

[edit] 5.2 Vektorproduct och skalär trippleprodukt

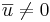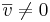Def2: Låt $\overline{u} \neq 0$ och $\overline{v} \neq 0$ vara två vektorer i rummet. Med vektorprodukt menas den vektor som har egenskapen:

$|\overline{v} \times \overline{v}| = |\overline{u}| \cdot |\overline{v}| \sin[\overline{u},\overline{v}]$ .
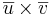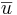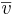$\overline{u} \times \overline{v}$ är ortogonal mot både $\overline{u}$ och $\overline{v}$ .
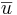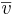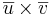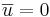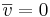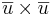De tre vektorena $\overline{u}$ , $\overline{v}$ och $\overline{u} \times \overline{v}$ är positivt orienterade om $\overline{u}= 0$ eller $\overline{v} = 0$ så är $\overline{u} \times \overline{u}$ = 0.

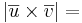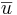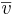Sats: $|\overline{u} \times \overline{v}| =$ arean av den parallellogram som representeras av $\overline{u}$ och $\overline{v}$ .

Def3: Med skalär trippelproduct menas 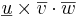$\underline{u} \times \overline{v} \cdot \overline{w}$ . Den ger Volumen av en låda med formlen:

$|\overline{u} \times \overline{v}| \cdot |\overline{w}| \cdot \cos[(\overline{u} \times \overline{v}),\overline{w}] = |(\overline{u} \times \overline{v}) \cdot \overline{w}|$

Detta gäller enbart om samtliga är posetivt orienterade eller samtliga är negativt orienterade.

[edit] 5.3 räknelagar för vektorprodukt

(i) 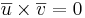$\overline{u} \times \overline{v} = 0$ endast om vektorena är parallella.
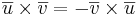
(ii) $\overline{u} \times \overline{v} = - \overline{v} \times \overline{u}$
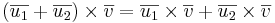
(iii) $(\overline{u_1} + \overline{u_2}) \times \overline{v} = \overline{u_1} \times \overline{v} + \overline{u_2} \times \overline{v}$
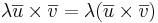
(iv) $\lambda\overline{u} \times \overline{v} = \lambda(\overline{u}\times\overline{v})$

[edit] 5.4 Vektorprodukt i ortonomerade baser

antag att 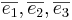$\overline{e_1}, \overline{e_2}, \overline{e_3}$ är en pos.orienterad bas i rummet. Då gäller:

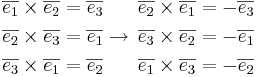
$\begin{align} \overline{e_1} \times \overline{e_2} = \overline{e_3} \\ \overline{e_2} \times \overline{e_3} = \overline{e_1} \\ \overline{e_3} \times \overline{e_1} = \overline{e_2} \end{align} \to \begin{align} \overline{e_2} \times \overline{e_1} = -\overline{e_3} \\ \overline{e_3} \times \overline{e_2} = -\overline{e_1} \\ \overline{e_1} \times \overline{e_3} = -\overline{e_2} \end{align}$

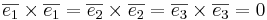
NOTE $\overline{e_1} \times \overline{e_1} = \overline{e_2} \times \overline{e_2} = \overline{e_3} \times \overline{e_3} = 0$

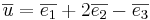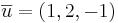
EX1: $\overline{u} = \overline{e_1} + 2\overline{e_2} - \overline{e_3}$ . $\overline{u} = (1,2,-1)$

Beräkna 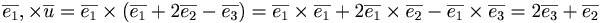$\overline{e_1}, \times \overline{u} = \overline{e_1} \times (\overline{e_1} + 2\overline{e_2} - \overline{e_3}) = \overline{e_1} \times \overline{e_1} + 2\overline{e_1} \times \overline{e_2} - \overline{e_1} \times \overline{e_3} = 2 \overline{e_3} + \overline{e_2}$

Alltså vektorn 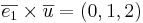$\overline{e_1} \times \overline{u} = (0,1,2)$ .

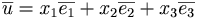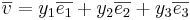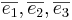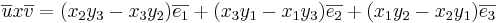Sats5: Om $\overline{u} = x_1 \overline{e_1} + x_2 \overline{e_2} + x_3 \overline{e_3}$ och $\overline{v} = y_1\overline{e_1} + y_2\overline{e_2} + y_3\overline{e_3}$ med avseende på en pos.orienterad bas $\overline{e_1},\overline{e_2},\overline{e_3}$ så är $\overline{u}x\overline{v} = (x_2y_3 - x_3y_2)\overline{e_1} + (x_3y_1 - x_1y_3)\overline{e_2} + (x_1y_2 - x_2y_1)\overline{e_3}$ .

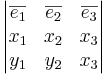
$\begin{vmatrix} \overline{e_1} & \overline{e_2} & \overline{e_3} \\ x_1 & x_2 & x_3 \\ y_1 & y_2 & x_3 \end{vmatrix}$

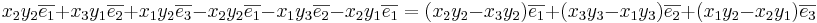
$x_2y_2\overline{e_1}+x_3y_1\overline{e_2}+x_1y_2\overline{e_3}-x_2y_2\overline{e_1}-x_1y_3\overline{e_2}-x_2y_1\overline{e_1} = (x_2y_2 - x_3y_2)\overline{e_1} + (x_3y_3 - x_1y_3)\overline{e_2} + (x_1y_2 - x_2y_1)\overline{e_3}$

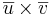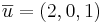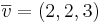EX1: Beräkna $\overline{u} \times \overline{v}$ när $\overline{u} = (2,0,1)$ och $\overline{v} = (2,2,3)$ .

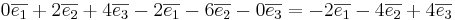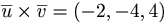svar: $0\overline{e_1} + 2\overline{e_2} + 4\overline{e_3} - 2\overline{e_1} - 6\overline{e_2} - 0\overline{e_3} = -2\overline{e_1} - 4\overline{e_2} + 4\overline{e_3}$ . $\overline{u} \times \overline{v} = (-2,-4,4)$ .

$π = - 2 x - 4 y + 4 z + d = 0$

[edit] 5.5 Några geometriska tillämpningar

EX1: Beräkna arean av triangelen med hörn i $P 0 :(2,2,1), P 1 :(4,3,2), P 2 :(1,5,1)$ .

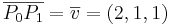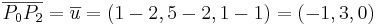$\overline{P_0P_1} = \overline{v} = (2,1,1)$ och $\overline{P_0P_2} = \overline{u} = (1-2,5-2,1-1) = (-1,3,0)$ .

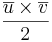
svar: $\frac{\overline{u} \times \overline{v}}{2}$

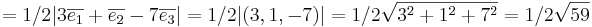
$= 1/2 |3\overline{e_1} + \overline{e_2} - 7\overline{e_3}| = 1/2 |(3,1,-7)| = 1/2 \sqrt{3^2+1^2+7^2} = 1/2 \sqrt{59}$

Vanligt tenta uppgift: EX: Avståndet mellan två linjer

[edit] Kvadratiska Linjära ekvationsystem

sats3: För kvadratiska matriser A är följande vilkor ekvivalanta.

A:s Kolonnvekktorer utgör en bas
AX = 0 har bara den triviala lösningen X = 0
AX=Y är lösbart för alla y

[edit] 7.5 Invers matris

Ekvationsystemet A: 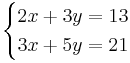$\begin{cases} 2x + 3y = 13 \\ 3x + 5y = 21 \end{cases}$

har lösningen 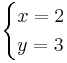$\begin{cases} x = 2 \\ y = 3 \end{cases}$

Lösningen kan även skrivas som 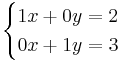$\begin{cases} 1x + 0y = 2 \\ 0x + 1y = 3 \end{cases}$

eller matrisform 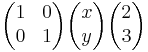$\begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} \begin{pmatrix} 2 \\ 3 \end{pmatrix}$

Invermatris skrivs som $A - 1$ .

Alltså: AX = Y

$A - 1 A X = A - 1 Y$ där $A - 1 A$ är I (Enhets matrisen).

Enhetsmatriser har utseendet

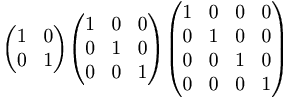
$\begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}$

Enhetsmatrisen fungera som en etta vid multiplikation.

EX IA = A

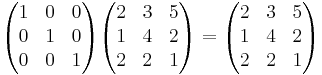
$\begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 2 & 3 & 5 \\ 1 & 4 & 2 \\ 2 & 2 & 1 \end{pmatrix} = \begin{pmatrix} 2 & 3 & 5 \\ 1 & 4 & 2 \\ 2 & 2 & 1 \end{pmatrix}$

Def: Den Kvadratiska matrisen A sägs vara inverterbar om det finns en matris $A - 1$ s"att $A - 1 A = I$ och A $A - 1 = I$ .

Matrisen $A - 1$ kallas inversen till matrisen A.

EX: A^-1 = 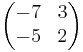$\begin{pmatrix} -7 & 3 \\ -5 & 2 \end{pmatrix}$ är invers till A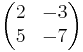 $\begin{pmatrix} 2 & -3 \\ 5 & -7 \end{pmatrix}$

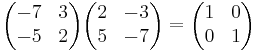
$\begin{pmatrix} -7 & 3 \\ -5 & 2 \end{pmatrix} \begin{pmatrix} 2 & -3 \\ 5 & -7 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}$

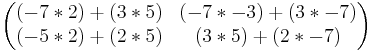
$\begin{pmatrix} (-7*2)+(3*5) & (-7*-3)+(3*-7) \\ (-5*2)+(2*5) & (3*5)+(2*-7) \end{pmatrix}$

Sats4. Om A och B är inverterbara så är $A - 1$ , $A t$ och AB inverterbara.

För inverserna gäller:

(i) $(A - 1) - 1 = A$
(ii) $(A T) - 1 = (A - 1) T$
(iii) $(A B) - 1 = B - 1 A - 1$ <-- Observera ordningen

Inversen kan beräknas:

EX: 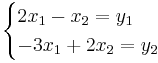$\begin{cases} 2 x_1 - x_2 = y_1 \\ -3 x_1 + 2 x_2 = y_2 \end{cases}$

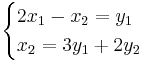
$\begin{cases} 2 x_1 - x_2 = y_1 \\ x_2 = 3y_1 + 2y_2 \\ \end{cases}$

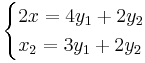
$\begin{cases} 2x = 4y_1 + 2y_2 \\ x_2 = 3y_1 + 2y_2 \end{cases}$

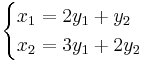
$\begin{cases} x_1 = 2y_1 + y_2 \\ x_2 = 3y_1 + 2y_2 \end{cases}$

Där 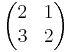$\begin{pmatrix} 2 & 1 \\ 3 & 2 \end{pmatrix}$ är inversen till A.

Om man kan lösa ett ekvationsystem AX = Y för ett allmänt högerled Y så är A inverterbart och gäller $A = A - 1 Y$

Där ett allmänt högreled är: 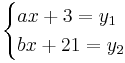$\begin{cases} ax + 3 = y_1 \\ bx + 21 = y_2 \end{cases}$

A = $\begin{pmatrix} 1 & 1 & 1 \\ 1 & 2 & 3 \\ 1 & 3 & 2 \end{pmatrix}$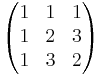

är inverterbar. Bestäm isåfall inversen:

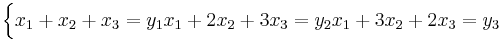
$\begin{cases} x_1 + x_2 + x_3 = y_1 x_1 + 2x_2 + 3x_3 = y_2 x_1 + 3x_2 + 2x_3 = y_3 \end{cases}$

Om $(x 1, x 2, x 3)$ går att lösa ut ur ekvationsystemet så finns det en invers.

Svar: 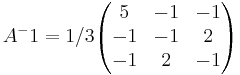$A^-1 = 1/3 \begin{pmatrix} 5 & -1 & -1 \\ -1 & -1 & 2 \\ -1 & 2 & -1 \end{pmatrix}$

[edit] 7.6 Matriser och basbyten

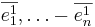Sats 6. Låt $\overline{e}_1, \ldots \overline{e_n}$ och $\overline{e_1^1}, \ldots -\overline{e_n^1}$ vara två baser i $R n$ .

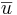Låt S vara matrisen som har kolonnvektorena $\overline{e_1^1}, \ldots \overline{e_n^1}$ . Antag att en vektor $\overline{u}$ har koordinatfranställningen 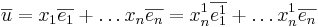$\overline{u} = x_1 \overline{e_1} + \ldots x_n \overline{e_n} = x_n^1 \overline{e_1^1} + \ldots x_n^1 \overline{e_n}$ . Då är X = SX' där X =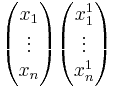 $\begin{pmatrix} x_1 \\ \vdots \\ x_n \end{pmatrix} \begin{pmatrix} x_1^1 \\ \vdots \\ x_n^1 \end{pmatrix}$

Matrisen S kallas för basbytesmatris!

OBS1 Basbytematriser är alltid inverterbara...

OBS2 Man är oftast intresserad av x' (man vet oftast redan vad x är).

$S - 1 X = S - 1 S X 1$ Där $S - 1 S = I$

$S 1 X = X 1$

$X 1 = S - 1 X$

EX: 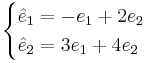$\begin{cases} \hat e_1 = -e_1 + 2e_2 \\ \hat e_2 = 3e_1 + 4e_2 \end{cases}$

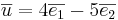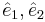Vilka koordinater har vektorn $\overline{u} = 4\overline{e_1} - 5\overline{e_2}$ i basen $\hat e_1 , \hat e_2$ ?

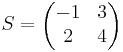
$S = \begin{pmatrix} -1 & 3 \\ 2 & 4 \end{pmatrix}$

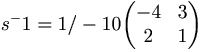
$s^-1 = 1 / -10 \begin{pmatrix} -4 & 3 \\ 2 & 1 \end{pmatrix}$

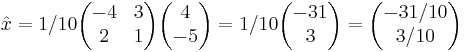
$\hat x = 1/10 \begin{pmatrix} -4 & 3 \\ 2 & 1 \end{pmatrix} \begin{pmatrix} 4 \\ -5 \end{pmatrix} = 1/10 \begin{pmatrix} -31 \\ 3 \end{pmatrix} = \begin{pmatrix} -31 / 10 \\ 3 / 10 \end{pmatrix}$

Def: A sägs vara en ortogonal matris om dess kolonnvektorer utgör en ortonomerad bas.

EX: Visa att matrisen A är ortogonal.

hint: ortogonal betyder att vektorena har längden 1 och är vinkelräta mot varandra.

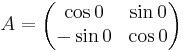
$A = \begin{pmatrix} \cos 0 & \sin 0 \\ -\sin 0 & \cos 0 \end{pmatrix}$

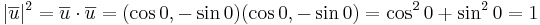
$|\overline{u}|^2 = \overline{u} \cdot \overline{u} = (\cos 0, -\sin 0) (\cos 0, -\sin0) = \cos^2 0 + \sin^2 0 = 1$

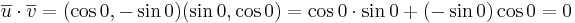
$\overline{u} \cdot \overline{v} = (\cos 0, -\sin 0) (\sin 0 , \cos 0) = \cos 0 \cdot \sin 0 + (-\sin 0) \cos 0 = 0$

EX: Bestäm talen a,b,c så att matrisen 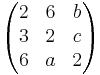$\begin{pmatrix} 2 & 6 & b \\ 3 & 2 & c \\ 6 & a & 2 \end{pmatrix}$ blir ortogonal.

hint Varje vektor ska vara vinkel rät med varandra dvs = med 0

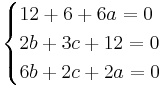
$\begin{cases} 12 + 6 + 6a = 0 \\ 2b + 3c + 12 = 0 \\ 6b + 2c + 2a = 0 \end{cases}$

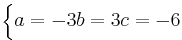
$\begin{cases} a = -3 b = 3 c = -6 \end{cases}$

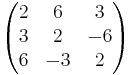
$\begin{pmatrix} 2 & 6 & 3 \\ 3 & 2 & -6 \\ 6 & -3 & 2 \end{pmatrix}$

Men som eftersom varje vektors längd är 7 så måste vi dividera med 7 på hela matrisen.

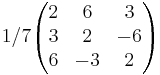
$1/7 \begin{pmatrix} 2 & 6 & 3 \\ 3 & 2 & -6 \\ 6 & -3 & 2 \end{pmatrix}$

är därav ortogonal!

Sats7: Följande villkor är ekvivalanta:

(i) Matrisen A är ortogonal
(ii) Kolonvektorena är en ortonomerad bas
(iii) Radvektorena är en ortonomerad bas
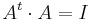
(iv) $A^t \cdot A = I$
(v) $A A T = I$
(vi) $A - 1 = A T$

[edit] Kap 8 linjära avbildningar

[edit] Funktionsbegreppet

Funktioner från R till R.

f (x) = x 2

-inte en linjär ekvation

f (x) = x

-En linjärfunktion

f (x) = a x

-En linjärfunktion

Linjära avbildningar handlar om motsvarigheter med flera variabler

EX:

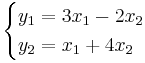$\begin{cases} y_1 = 3x_1 - 2x_2 \\ y_2 = x_1 + 4x_2 \end{cases}$ Vilket är en funktion från $R 2$ till $R 2$

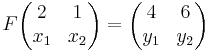
$F \begin{pmatrix} 2 & 1 \\ x_1 & x_2 \end{pmatrix} = \begin{pmatrix} 4 & 6 \\ y_1 & y_2 \end{pmatrix}$

F kan skrivas på matrisform.

$y = A X$

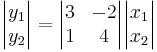
$\begin{vmatrix} y_1 \\ y_2 \end{vmatrix} = \begin{vmatrix} 3 & -2 \\ 1 & 4 \end{vmatrix} \begin{vmatrix} x_1 \\ x_2 \end{vmatrix}$

att 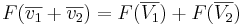$F(\overline{v_1}+\overline{v_2}) = F(\overline{V_1}) + F(\overline{V_2})$ för linjära avbildningar gäller även att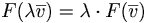 $F(\lambda\overline{v}) = \lambda \cdot F(\overline{v})$

EX: Betrakta den ortogonala Projecktionen på $4 X 1 - 3 X 2 = 0$

a) Var Projiceras (1,0) resp (0,1)

Skriv linjen på parameterform.

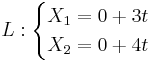
$L : \begin{cases} X_1 = 0 + 3t \\ X_2 = 0 + 4t \end{cases}$

$(L :(0,0) + t (3,4))$

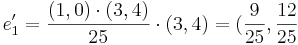
$e_1' = \frac{(1,0) \cdot (3,4)}{25} \cdot (3,4) = (\frac{9}{25},\frac{12}{25}$

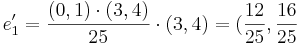
$e_1' = \frac{(0,1) \cdot (3,4)}{25} \cdot (3,4) = (\frac{12}{25},\frac{16}{25}$

[edit] Matrissambanden

b) Bestäm Matrissambandet y = A X

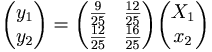
$\begin{pmatrix} y_1 \\ y_2 \end{pmatrix} = \begin{pmatrix} \frac{9}{25} & \frac{12}{25} \\ \frac{12}{25} & \frac{16}{25} \end{pmatrix} \begin{pmatrix} X_1 \\ x_2 \end{pmatrix}$

c)

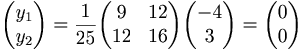
$\begin{pmatrix} y_1 \\ y_2 \end{pmatrix} = \frac{1}{25}\begin{pmatrix} 9 & 12 \\ 12 & 16 \end{pmatrix} \begin{pmatrix} -4 \\ 3 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \end{pmatrix}$

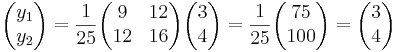
$\begin{pmatrix} y_1 \\ y_2 \end{pmatrix} = \frac{1}{25}\begin{pmatrix} 9 & 12 \\ 12 & 16 \end{pmatrix} \begin{pmatrix} 3 \\ 4 \end{pmatrix} = \frac{1}{25}\begin{pmatrix} 75 \\ 100 \end{pmatrix} = \begin{pmatrix} 3 \\ 4 \end{pmatrix}$

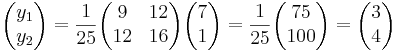
$\begin{pmatrix} y_1 \\ y_2 \end{pmatrix} = \frac{1}{25}\begin{pmatrix} 9 & 12 \\ 12 & 16 \end{pmatrix} \begin{pmatrix} 7 \\ 1 \end{pmatrix} = \frac{1}{25}\begin{pmatrix} 75 \\ 100 \end{pmatrix} = \begin{pmatrix} 3 \\ 4 \end{pmatrix}$

EX: Låt L vara linjen som går genom punkten O och har riktningsvektorn 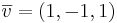$\overline{v} = (1,-1,1)$ . Låt P vara en godtycklig punkt i rummet och låt Q vara den ortogonala projektionen av P på L.

a) Sätt 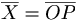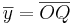$\overline{X} = \overline{OP}$ , $\overline{y} = \overline{OQ}$ härled en formel som beskriver avbildningen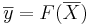 $\overline{y} = F(\overline{X})$

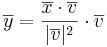
$\overline{y} = \frac{\overline{x} \cdot \overline{v}}{|\overline{v}|^2} \cdot \overline{v}$

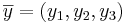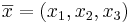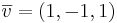b) Inför ett ortonomerat koordinatsystem i rummet med origo i punkten O. Bestäm koordinatsambandet mellan $\overline{y} = (y_1,y_2,y_3)$ och $\overline{x} = (x_1,x_2,x_3)$ om $\overline{v} = (1,-1,1)$ .

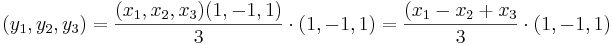
$(y_1,y_2,y_3) = \frac{(x_1,x_2,x_3)(1,-1,1)}{3} \cdot (1,-1,1) = \frac{(x_1 - x_2 + x_3}{3} \cdot (1,-1,1)$

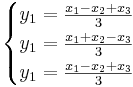
$\begin{cases} y_1 = \frac{x_1 - x_2 + x_3}{3} \\ y_1 = \frac{x_1 + x_2 - x_3}{3} \\ y_1 = \frac{x_1 - x_2 + x_3}{3} \end{cases}$

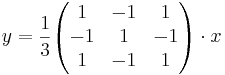
$y = \frac{1}{3} \begin{pmatrix} 1 & -1 & 1 \\ -1 & 1 & -1 \\ 1 & -1 & 1 \end{pmatrix} \cdot x$

alternativ sätt: Ta fram avbildningsmatrisen genom att kontrollera hur enhetsvektorena avbildas.

EX: Låt $(y 1, y 2, y 3)$ vara spegelbilden av $(x 1, x 2, x 3)$ vid spegling i planet $2 x 1 + x 2 - 2 x 3 = 0$ . Ange ett matrissamband mellan $(y 1, y 2, y 3)$ och $x 1, x 2, x 3)$ .

P :(x 1, x 2, x 3)

$\overline{n} = (2,1,-2)$

Q :(y 1, y 2, y 3)

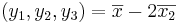
$(y_1,y_2,y_3) = \overline{x} - 2 \overline{x_2}$

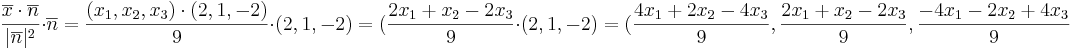
$\frac{\overline{x} \cdot \overline{n}}{|\overline{n}|^2} \cdot \overline{n} = \frac{(x_1,x_2,x_3) \cdot (2,1,-2)}{9} \cdot (2,1,-2) = (\frac{2x_1 + x_2 - 2x_3}{9} \cdot (2,1,-2) = (\frac{4x_1 + 2x_2 - 4x_3}{9},\frac{2x_1 + x_2 - 2x_3}{9},\frac{-4x_1 - 2x_2 + 4x_3}{9}$

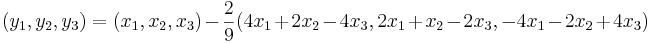$(y_1,y_2,y_3) = (x_1,x_2,x_3) - \frac{2}{9} (4x_1 + 2x_2 - 4x_3, 2x_1 + x_2 - 2x_3, -4x_1 -2x_2 + 4x_3)$ - Eftersom den ska till den andra sidan av speglingen, kan vi multiplicera med 2 på 1/9.

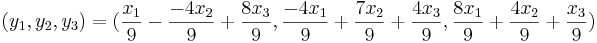
$(y_1,y_2,y_3) = (\frac{x_1}{9} - \frac{-4x_2}{9} + \frac{8x_3}{9}, \frac{-4x_1}{9} + \frac{7x_2}{9} + \frac{4x_3}{9}, \frac{8x_1}{9} + \frac{4x_2}{9} + \frac{x_3}{9})$

Alltså: 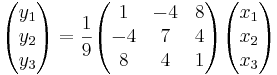$\begin{pmatrix} y_1 \\ y_2 \\ y_3 \end{pmatrix} = \frac{1}{9} \begin{pmatrix} 1 & -4 & 8 \\ -4 & 7 & 4 \\ 8 & 4 & 1 \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix}$

Alternativ:

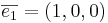$\overline{e_1} = (1,0,0)$ avbildas på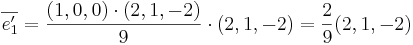 $\overline{e_1'} = \frac{(1,0,0) \cdot (2,1,-2)}{9} \cdot (2,1,-2) = \frac{2}{9} (2,1,-2)$

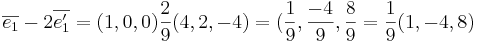
$\overline{e_1} - 2\overline{e_1'} = (1,0,0) \frac{2}{9} (4,2,-4) = (\frac{1}{9}, \frac{-4}{9}, \frac{8}{9} = \frac{1}{9}(1,-4,8)$

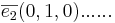
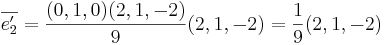
$\overline{e_2} (0,1,0)......$ $\overline{e_2'} = \frac{(0,1,0)(2,1,-2)}{9}(2,1,-2) = \frac{1}{9}(2,1,-2)$

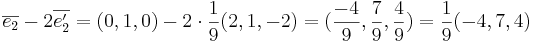
$\overline{e_2} - 2\overline{e_2'} = (0,1,0) - 2 \cdot \frac{1}{9}(2,1,-2) = (\frac{-4}{9}, \frac{7}{9}, \frac{4}{9}) = \frac{1}{9} (-4,7,4)$

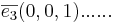
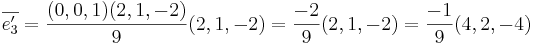
$\overline{e_3} (0,0,1)......$ $\overline{e_3'} = \frac{(0,0,1)(2,1,-2)}{9}(2,1,-2) = \frac{-2}{9}(2,1,-2) = \frac{-1}{9}(4,2,-4)$

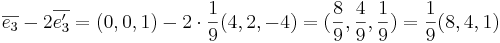
$\overline{e_3} - 2\overline{e_3'} = (0,0,1) - 2 \cdot \frac{1}{9}(4,2,-4) = (\frac{8}{9}, \frac{4}{9}, \frac{1}{9}) = \frac{1}{9} (8,4,1)$

Sats 1: Följande påstående är ekvivalenta:

(i) 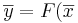$\overline{y} = F(\overline{x}$ där F är en linjär avbildning
(ii) y = ax där A är en rektangulär matris
(iii) A:s kolonner är bilderna av basvektorena
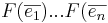
- d.v.s $F(\overline{e_1}) ... F(\overline{e_n}$

Def: Matrisen A i satsen kallas Avbildningsmatrisen för F där F är en funktion från N till M.

EX: $R 2$ till $R 3$ , vanligen $R 2$ till $R 2$ eller $R 3$ till $R 3$ . (plannet till plannet, rummet till rummet, planet till planet...)

OBS! Satsen säger att det räker att veta hur F avbildar enhetsvektorena.

OBS! Definitioner av linjära avbildning bygger på funktioner av vektorer när det gäller avbildning av punkter "går man över" och räknar med ortsvektorer.

EX: Projicera rummets punkter i planet $π: x 1 - 2 x 2 + 2 x 3 = 0$ . Alltså bestäm en matris för skuggor om ljuset kommer från solen i riktningen 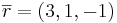$\overline{r} = (3,1,-1)$ . skugga punkten P : (7,8,2).

$y = A x$

[edit] Hur avbildas en enhetsvektorena?

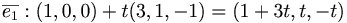
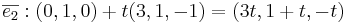
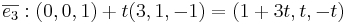
$\overline{e_1} : (1,0,0) + t(3,1,-1) = (1 + 3t, t, -t)$ $\overline{e_2} : (0,1,0) + t(3,1,-1) = (3t, 1+ t, -t)$ $\overline{e_3} : (0,0,1) + t(3,1,-1) = (1 + 3t, t, -t)$

Alltså: $x 1 - 2 x 2 + 2 x 3 = 0$

1 + 3 t - 2(t) + 2( - t) = 0

1 - t = 0

t = 1

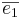$\overline{e_1}$ avbildas på $(1 + 3,1, - 1) = (4,1, - 1)$

t = 1

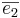$\overline{e_2}$ avbildas på $( - 6, - 1,2)$

t = - 2

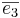$\overline{e_3}$ avbildas på $(6,2, - 1)$

t = 2

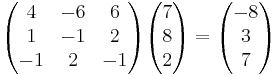
$\begin{pmatrix} 4 & -6 & 6 \\ 1 & -1 & 2 \\ -1 & 2 & -1 \end{pmatrix} \begin{pmatrix} 7 \\ 8 \\ 2 \end{pmatrix} = \begin{pmatrix} -8 \\ 3 \\ 7 \end{pmatrix}$

EX: Spegla punkten P : (1,1,1,) i planet $π:3 x + 4 y - 2 z = 0$

$(1,1,1,) + t (3,4, - 2) = (1 + 3 t,1 + 4 t,1 - 2 t)$

$3(1 + 3 t) + 4(1 + 4 t) - 2(1 - 2 t) = 0$

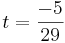
$t = \frac{-5}{29}$

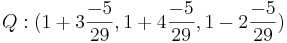
$Q : (1 + 3\frac{-5}{29}, 1 + 4\frac{-5}{29}, 1 - 2\frac{-5}{29})$

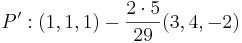
$P' : (1,1,1) - \frac{2 \cdot 5}{29} (3,4,-2)$

[edit] 2007-10-05

[edit] Avbildnings vektorer

[edit] Exempel på att skapa en avbildnings vektor

EX Utgå från en känd vektor 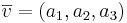$\overline{v} = (a_1,a_2,a_3)$ I rummet. Betrakta den linjära avbildningen:

$y \times x$

Ange ett matrissamband för avbildningen. Alltså:

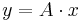
$y = A \cdot x$

TipsKontrollea vad som händer med enhetsvektorena vid avbildningen. 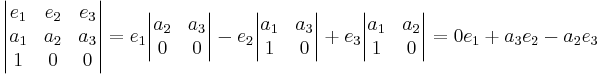$\begin{vmatrix} e_1 & e_2 & e_3 \\ a_1 & a_2 & a_3 \\ 1 & 0 & 0 \end{vmatrix} = e_1 \begin{vmatrix} a_2 & a_3 \\ 0 & 0 \end{vmatrix} - e_2 \begin{vmatrix} a_1 & a_3 \\ 1 & 0 \end{vmatrix} + e_3 \begin{vmatrix} a_1 & a_2 \\ 1 & 0 \end{vmatrix} = 0e_1 + a_3e_2 - a_2e_3$

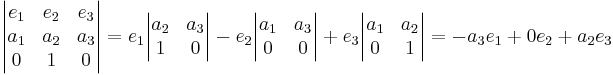
$\begin{vmatrix} e_1 & e_2 & e_3 \\ a_1 & a_2 & a_3 \\ 0 & 1 & 0 \end{vmatrix} = e_1 \begin{vmatrix} a_2 & a_3 \\ 1 & 0 \end{vmatrix} - e_2 \begin{vmatrix} a_1 & a_3 \\ 0 & 0 \end{vmatrix} + e_3 \begin{vmatrix} a_1 & a_2 \\ 0 & 1 \end{vmatrix} = -a_3e_1 + 0e_2 + a_2e_3$

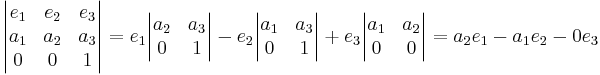
$\begin{vmatrix} e_1 & e_2 & e_3 \\ a_1 & a_2 & a_3 \\ 0 & 0 & 1 \end{vmatrix} = e_1 \begin{vmatrix} a_2 & a_3 \\ 0 & 1 \end{vmatrix} - e_2 \begin{vmatrix} a_1 & a_3 \\ 0 & 1 \end{vmatrix} + e_3 \begin{vmatrix} a_1 & a_2 \\ 0 & 0 \end{vmatrix} = a_2e_1 - a_1e_2 - 0e_3$

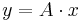
$y = A \cdot x$

[edit] Svar

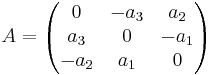
$A = \begin{pmatrix} 0 & -a_3 & a_2 \\ a_3 & 0 & -a_1 \\ -a_2 & a_1 & 0 \end{pmatrix}$

[edit] Matriser för speciella avbildningar

Sats: Den linjära avbildningen ortogonal projektion på vektorn 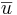$\overline{u}$ har avbildningsmatrisen:

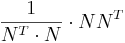
$\frac{1}{N^T \cdot N} \cdot N N^T$

där N är kolonnmatrisen som motsvarar 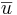$\overline{u}$ .

EX: om N = (1,-1,1)

Hint: matris multiplikation

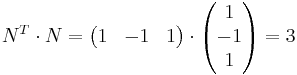
$N^T \cdot N = \begin{pmatrix} 1 & -1 & 1 \end{pmatrix} \cdot \begin{pmatrix} 1 \\ -1 \\ 1 \end{pmatrix} = 3$

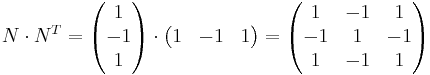
$N \cdot N^T = \begin{pmatrix} 1 \\ -1 \\ 1 \end{pmatrix} \cdot \begin{pmatrix} 1 & -1 & 1 \end{pmatrix} = \begin{pmatrix} 1 & -1 & 1 \\ -1 & 1 & -1 \\ 1 & -1 & 1 \end{pmatrix}$

[edit] = Matrissamband

EX: Bestäm ett matrissamband mellan $(y 1, y 2)$ och $(x 1, x 2)$ om $(x 1, x 2)$ övergår i $(y 1, y 2)$ efter vridning 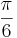$\frac{\pi}{6}$ i positivt led.

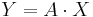
$Y = A \cdot X$

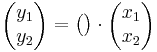
$\begin{pmatrix} y_1 \\ y_2 \end{pmatrix} = \begin{pmatrix} \\ \end{pmatrix} \cdot \begin{pmatrix} x_1 \\ x_2 \end{pmatrix}$

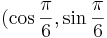
$(\cos \frac{\pi}{6}, \sin \frac{\pi}{6}$

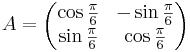
$A = \begin{pmatrix} \cos \frac{\pi}{6} & -\sin \frac{\pi}{6} \\ \sin \frac{\pi}{6} & \cos \frac{\pi}{6} \end{pmatrix}$

[edit] Isometrisk avbildning

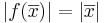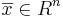Definition: En linjär avbildning sägs vara isometrisk om $|f(\overline{x})| = |\overline{x}|$ för alla $\overline{x} \in R^n$ .

Sats: En linjär avbildning är isometrisk om och endast om dess avbildningsmatris är ortogonal.

Värdemängd: Är mängden av alla 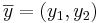$\overline{y} = (y_1,y_2)$ som funktionen kan generera.

Vid projektion på en linje är värdemängden hela linjen.
Vid spegling i plan är värdemängden hela rummet.
Vid Projektion i ett plan är värdemängden hela planet.

[edit] Sammansättning av två funktioner

Vanlig sista tenta uppgift

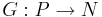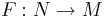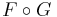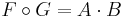
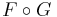Sats: Om två avbildningar $G : P \to N$ och $F : N \to M$ är linjära så är även $F \circ G$ linjära. Om F har avbildningsmatrisen A och G har avbildningsmatrisen B så gäller $F \circ G = A \cdot B$

$F \circ G$ betyder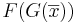 $F(G(\overline{x}))$

Tips Dens avbildningsmatris som utförs först, ska stå sist i 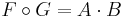$F \circ G = A \cdot B$

EX: Bestäm matrisen för den avbildning som erhålls genom att man roterar planets punkter med vinkeln 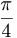$\frac{\pi}{4}$ runt origo och därefter speglar punkterna i x-axeln.

Funktionen G rotera med matrisen B.
Funktionen F speglar med matrisen A.

Rotation 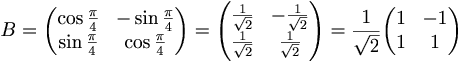$B = \begin{pmatrix} \cos \frac{\pi}{4} & - \sin \frac{\pi}{4} \\ \sin \frac{\pi}{4} & \cos \frac{\pi}{4} \end{pmatrix} = \begin{pmatrix} \frac{1}{\sqrt{2}} & - \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{pmatrix} = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 & -1 \\ 1 & 1 \end{pmatrix}$

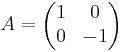
$A = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}$

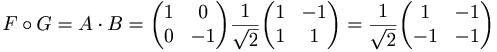
$F \circ G = A \cdot B = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} \frac{1}{\sqrt{2}} \begin{pmatrix} 1 & -1 \\ 1 & 1 \end{pmatrix} = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 & -1 \\ -1 & -1 \end{pmatrix}$

[edit] EX

Ett rörsystem med tillflöde $x 1, x 2$ och uttflöde $(y 1, y 2, y 3)$ .

Utflödet är alltså en funktion av tillflöde. Alltså en funktion från 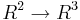$R^2 \to R^3$

$y 1 = a 11 x 1 + a 12 x 2$ $y 2 = a 21 x 1 + a 22 x 2$ $y 3 = a 31 x 1 + a 32 x 2$

Vid mätningar erhölls följande utflöden:

Då x₁ = 1 och x₂ = 0:
- $y_1 = \frac{1}{5}$
- $y_2 = \frac{2}{5}$
- $y_3 = \frac{2}{5}$
Då x₁ = 0 och x₂ = 1:
- $y_1 = \frac{1}{4}$
- $y_2 = \frac{1}{2}$
- $y_3 = \frac{1}{4}$

Hur stor blir utflödet om $x 1 = 3$ och $x 2 = 4$ ?

[edit] Svar:

$Y = A X$ där Y = 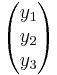$\begin{pmatrix} y_1 \\ y_2 \\ y_3 \end{pmatrix}$ och X =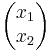 $\begin{pmatrix} x_1 \\ x_2 \end{pmatrix}$

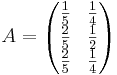
$A = \begin{pmatrix} \frac{1}{5} & \frac{1}{4} \\ \frac{2}{5} & \frac{1}{2} \\ \frac{2}{5} & \frac{1}{4} \end{pmatrix}$

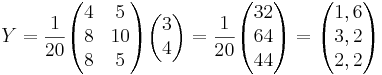
$Y = \frac{1}{20} \begin{pmatrix} 4 & 5 \\ 8 & 10 \\ 8 & 5 \end{pmatrix} \begin{pmatrix} 3 \\ 4 \end{pmatrix} = \frac{1}{20} \begin{pmatrix} 32 \\ 64 \\ 44 \end{pmatrix} = \begin{pmatrix} 1,6 \\ 3,2 \\ 2,2 \end{pmatrix}$

[edit] Gammla tenta uppgifter

[edit] Lös ekv.

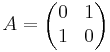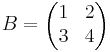
$A B X + B = A B$ där $A = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}$ och $B = \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix}$

A B X + B = A B

(A B) X = A B - B

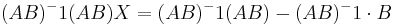
$(A B)^-1 (A B) X = (A B)^-1 (A B) - (A B)^-1 \cdot B$

I = (A B) - 1(A B)

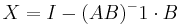
$X = I - (A B)^-1 \cdot B$

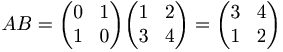
$A B = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} = \begin{pmatrix} 3 & 4 \\ 1 & 2 \end{pmatrix}$

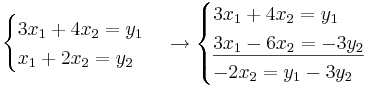
$\begin{cases} 3x_1 + 4x_2 = y_1 \\ x_1 + 2x_2 = y_2 \end{cases} \to \begin{cases} 3x_1 + 4x_2 = y_1 \\ \underline{3x_1 - 6x_2 = -3y_2} \\ -2x_2 = y_1 - 3y_2 \end{cases}$

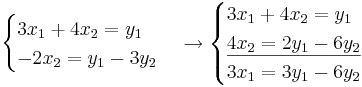
$\begin{cases} 3x_1 + 4x_2 = y_1 \\ -2x_2 = y_1 - 3y_2 \end{cases} \to \begin{cases} 3x_1 + 4x_2 = y_1 \\ \underline{4x_2 = 2y_1 - 6y_2} \\ 3x_1 = 3y_1 - 6y_2 \end{cases}$

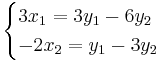
$\begin{cases} 3x_1 = 3y_1 - 6y_2 \\ -2x_2 = y_1 - 3y_2 \end{cases}$

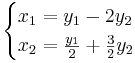
$\begin{cases} x_1 = y_1 - 2y_2 \\ x_2 = \frac{y_1}{2} + \frac{3}{2}y_2 \end{cases}$

Inversen blir: 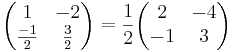$\begin{pmatrix} 1 & -2 \\ \frac{-1}{2} & \frac{3}{2} \end{pmatrix} = \frac{1}{2} \begin{pmatrix} 2 & -4 \\ -1 & 3 \end{pmatrix}$

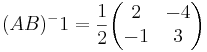
$(A B)^-1 = \frac{1}{2} \begin{pmatrix} 2 & -4 \\ -1 & 3 \end{pmatrix}$

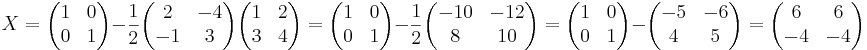
$X = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} - \frac{1}{2} \begin{pmatrix} 2 & -4 \\ -1 & 3 \end{pmatrix} \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} - \frac{1}{2} \begin{pmatrix} -10 & -12 \\ 8 & 10 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} - \begin{pmatrix} -5 & -6 \\ 4 & 5 \end{pmatrix} = \begin{pmatrix} 6 & 6 \\ -4 & -4 \end{pmatrix}$

[edit] Betrakta basbytet:

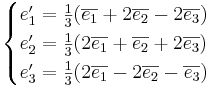
$\begin{cases} e'_1 = \frac{1}{3} (\overline{e_1} + 2 \overline{e_2} - 2 \overline{e_3}) \\ e'_2 = \frac{1}{3} (2 \overline{e_1} + \overline{e_2} + 2 \overline{e_3}) \\ e'_3 = \frac{1}{3} (2 \overline{e_1} - 2 \overline{e_2} - \overline{e_3}) \end{cases}$

Ett plan har ekvationen $x' + 2 y' + 3 z' = 0$ i basen 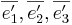$\overline{e'_1},\overline{e'_2},\overline{e'_3}$ .

Bestäm planets ekvation i basen 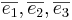$\overline{e_1},\overline{e_2},\overline{e_3}$ .

$X = S X'$

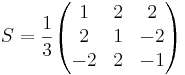
$S = \frac{1}{3} \begin{pmatrix} 1 & 2 & 2 \\ 2 & 1 & -2 \\ -2 & 2 & -1 \\ \end{pmatrix}$

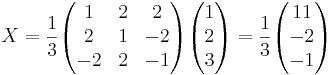
$X = \frac{1}{3} \begin{pmatrix} 1 & 2 & 2 \\ 2 & 1 & -2 \\ -2 & 2 & -1 \\ \end{pmatrix} \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} = \frac{1}{3} \begin{pmatrix} 11 \\ -2 \\ -1 \end{pmatrix}$

[edit] SVAR

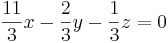
$\frac{11}{3} x - \frac{2}{3} y - \frac{1}{3} z = 0$

$11 x - 2 y - z = 0$

[edit] Muterad variant

Vi vet att svaret är $11 x - 2 y - z = 0$

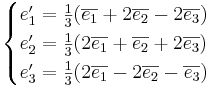
$\begin{cases} e'_1 = \frac{1}{3} (\overline{e_1} + 2 \overline{e_2} - 2 \overline{e_3}) \\ e'_2 = \frac{1}{3} (2 \overline{e_1} + \overline{e_2} + 2 \overline{e_3}) \\ e'_3 = \frac{1}{3} (2 \overline{e_1} - 2 \overline{e_2} - \overline{e_3}) \end{cases}$

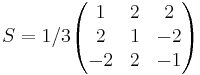
$S = 1/3 \begin{pmatrix} 1 & 2 & 2 \\ 2 & 1 & -2 \\ -2 & 2 & -1 \end{pmatrix}$

$S - 1 X = S - 1 S X'$

$S - 1 S = I$

$s - 1 X = X'$

$X' = S - 1 X$

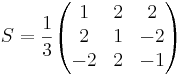
$S = \frac{1}{3} \begin{pmatrix} 1 & 2 & 2 \\ 2 & 1 & -2 \\ -2 & 2 & -1 \end{pmatrix}$

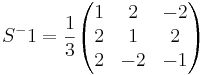
$S^-1 = \frac{1}{3} \begin{pmatrix} 1 & 2 & -2 \\ 2 & 1 & 2 \\ 2 & -2 & -1 \end{pmatrix}$

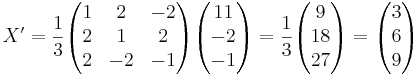
$X' = \frac{1}{3} \begin{pmatrix} 1 & 2 & -2 \\ 2 & 1 & 2 \\ 2 & -2 & -1 \end{pmatrix} \begin{pmatrix} 11 \\ -2 \\ -1 \end{pmatrix} = \frac{1}{3} \begin{pmatrix} 9 \\ 18 \\ 27 \end{pmatrix} = \begin{pmatrix} 3 \\ 6 \\ 9 \end{pmatrix}$

$3 x + 6 y + 9 z = 0$

$x + 2 y + 3 z = 0$

[edit] 2007-10-10

[edit] Kap 9. Determinanter

För kvadratiska matriser (A) inför man ett tal med determinanten A (det A).

EX 1:

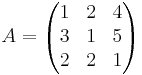
$A = \begin{pmatrix} 1 & 2 & 4 \\ 3 & 1 & 5 \\ 2 & 2 & 1 \end{pmatrix}$

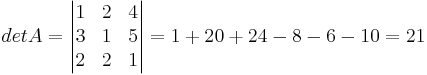
$det A = \begin{vmatrix} 1 & 2 & 4 \\ 3 & 1 & 5 \\ 2 & 2 & 1 \end{vmatrix} = 1+ 20 + 24 - 8 - 6 - 10 = 21$

EX 2:

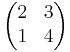
$\begin{pmatrix} 2 & 3 \\ 1 & 4 \end{pmatrix}$

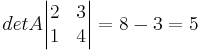
$det A \begin{vmatrix} 2 & 3 \\ 1 & 4 \end{vmatrix} = 8 - 3 = 5$

[edit] 9.1

Parallellepiped = En "låda" uppspänd med rums vektorena.

Volym av en parallellepiped med tecken $V(\overline{a_1},\overline{a_2}, \overline{a_3} = \begin{cases} w(\overline{a_1}, \overline{a_2}, \overline{a_3}) \mbox{om }(\overline{a_1}, \overline{a_2}, \overline{a_3}) \mbox{är posetivt orienterade }\\\\ -w(...) \mbox{är posetivt orienterade } \end{cases}$

Volymsatsen. Låt 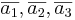$\overline{a_1}, \overline{a_2}, \overline{a_3}$ vara matrisen A:s kolonnvektorer med avseende på basen 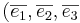$(\overline{e_1}, \overline{e_2}, \overline{e_3}$ dvs:

$\overline{a_1} = a_11 \overline{e_1} + a_21 \overline{e_2} + a_31 \overline{e_3}$

$\overline{a_2} = a_12 \overline{e_1} + a_22 \overline{e_2} + a_32 \overline{e_3}$

$\overline{a_3} = a_13 \overline{e_1} + a_23 \overline{e_2} + a_33 \overline{e_3}$

Då gäller 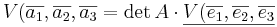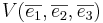$V(\overline{a_1}, \overline{a_2}, \overline{a_3} = \det A \cdot \underline{V(\overline{e_1}, \overline{e_2}, \overline{e_3}}$ . $V(\overline{e_1}, \overline{e_2}, \overline{e_3})$ kan betraktas som en volymsenhet.

Följdsats: Antag att A:s kolonnvektorer är 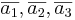$\overline{a_1}, \overline{a_2}, \overline{a_3}$ då gäller det 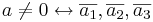$a \neq 0 \leftrightarrow \overline{a_1}, \overline{a_2}, \overline{a_3}$ är linjärt oberoende och det 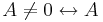$A \neq 0 \leftrightarrow A$ är inverterbar.

EX 1: Vektorena 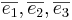$\overline{e_1}, \overline{e_2}, \overline{e_3}$ utgör en bas för rummets vektorer, med egenskapen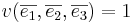 $v(\overline{e_1}, \overline{e_2}, \overline{e_3}) = 1$

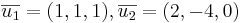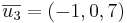
Bestäm volymen av den parallellepiped som spänns up av $\overline{u_1} = (1,1,1), \overline{u_2} = (2,-4,0)$ och $\overline{u_3} = (-1,0,7)$

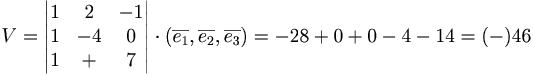
$V = \begin{vmatrix} 1 & 2 & -1 \\ 1 & -4 & 0 \\ 1 & + & 7 \\ \end{vmatrix} \cdot (\overline{e_1}, \overline{e_2}, \overline{e_3}) = -28 + 0 + 0 - 4 - 14 = (-)46$

svaret är att volymen är 46 v.e

EX 2:

En parallellepiped har ett hörn i origo och de tre närligande hörnen i punkterna (3,0,-3), (6, 3, z) och (3,3,6). bestäm z så att parallellepiped volymen blir 27 volymenheter.

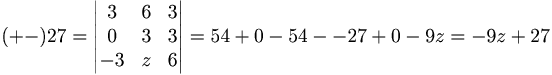
$(+-)27 = \begin{vmatrix} 3 & 6 & 3 \\ 0 & 3 & 3 \\ -3 & z & 6 \end{vmatrix} = 54 + 0 - 54 - -27 + 0 -9z = -9z + 27$

svar: $- 9 z + 27 = 27$ och $- 9 z + 27 = - 27$

EX 3:

Bestäm arean av en triangel med hörnen i (-1,2), (2,1) och (3,3).

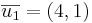
$\overline{u_1} = (4,1)$

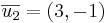
$\overline{u_2} = (3,-1)$

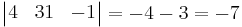
$\begin{vmatrix} 4 & 3 1 & -1 \end{vmatrix} = -4 - 3 = -7$

Triangelarean är 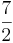$\frac{7}{2}$ a.e

EX 4:

Beräkna volymen av en tetraceder med hörn i punkterna $P 0 (0,0,0), P 1 (1,0, - 1), P 2 (2,1,0)$ och $P 3 (1,1,2)$

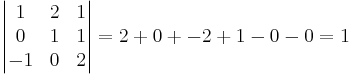
$\begin{vmatrix} 1 & 2 & 1 \\ 0 & 1 & 1 \\ -1 & 0 & 2 \end{vmatrix} = 2 + 0 + -2 + 1 - 0 - 0 = 1$

Volymen blir 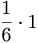$\frac{1}{6} \cdot 1$ V.e

Sats 2. För varje kvadratisk (A) Matris råder sambandet det A = det $A T$

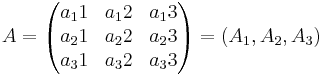
$A = \begin{pmatrix} a_11 & a_12 & a_13 \\ a_21 & a_22 & a_23 \\ a_31 & a_32 & a_33 \end{pmatrix} = (A_1,A_2,A_3)$

där $A 1, A 2, A 3$ är vektorena

Sats3. För determinanter gäller följande räknerelagar

a) det

(A' 1 + A'' 1, A 2, A 3) = det(A' 1, A 2, A 3) + det(A'' 1, A 2, A 3)

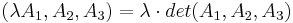
b) det $(\lambda A_1, A_2, A_3) = \lambda \cdot det (A_1,A_2,A_3)$

c) om två kolonner byter plats så ändras determinanten tecken

d) om två kolonner är lika så är determinanten noll.

e) adderar man en mulltipel av en kolonn till en annan kolonn så ändras ej determinanten.

EX: det 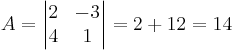$A = \begin{vmatrix} 2 & -3 \\ 4 & 1 \end{vmatrix} =2 + 12 = 14$

Om $A 1 = A' 1 + A'' 2$

a)

det A = 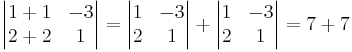$\begin{vmatrix} 1+1 & -3 \\ 2 + 2 & 1 \end{vmatrix} = \begin{vmatrix} 1 & -3 \\ 2 & 1 \end{vmatrix} + \begin{vmatrix} 1 & -3 \\ 2 & 1 \end{vmatrix} = 7 + 7$

b)

$λ = 3$

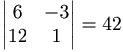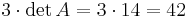
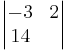
$\begin{vmatrix} 6 & -3 \\ 12 & 1 \end{vmatrix} = 42$ är samma sak som $3 \cdot \det A = 3 \cdot 14 = 42$

c)

$\begin{vmatrix} -3 & 2 \\ 1 4 \end{vmatrix}$

d)

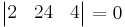
$\begin{vmatrix} 2 & 2 4 & 4 \end{vmatrix} = 0$

e)

$\begin{vmatrix} 2 & -3 \\ 4 & 1 \end{vmatrix} = \begin{vmatrix} -4 & -3 \\ 6 & 1 \end{vmatrix}$

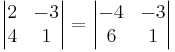
EX:

Beräkna följande determinanter

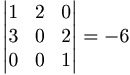
a) $\begin{vmatrix} 1 & 2 & 0 \\ 3 & 0 & 2 \\ 0 & 0 & 1 \end{vmatrix} = -6$

b)

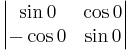
$\begin{vmatrix} \sin 0 & \cos 0 \\ -\cos 0 & \sin 0 \end{vmatrix}$

EX: lös ekvationen 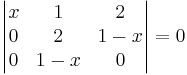$\begin{vmatrix} x & 1 & 2 \\ 0 & 2 & 1-x \\ 0 & 1-x & 0 \end{vmatrix} = 0$

svar: $x (x - 1) 2 = 0, X = 1$

Utveckling av determinant efter rad och koloun

EX: Beräkna

det 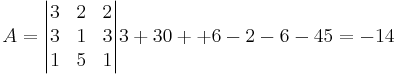$A = \begin{vmatrix} 3 & 2 & 2 \\ 3 & 1 & 3 \\ 1 & 5 & 1 \end{vmatrix} 3 + 30 + + 6 - 2 - 6 - 45 = - 14$

det 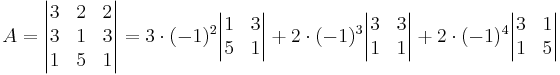$A = \begin{vmatrix} 3 & 2 & 2 \\ 3 & 1 & 3 \\ 1 & 5 & 1 \end{vmatrix} = 3 \cdot (-1)^2 \begin{vmatrix} 1 & 3 \\ 5 & 1 \end{vmatrix} + 2\cdot (-1)^3\begin{vmatrix} 3 & 3 \\ 1 & 1 \end{vmatrix} + 2\cdot (-1)^4\begin{vmatrix} 3 & 1 \\ 1 & 5 \end{vmatrix}$

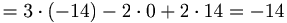
$= 3 \cdot (-14) - 2 \cdot 0 + 2 \cdot 14 = -14$

Beräkna determenanten A genom att utveckla efter kolonn 2.

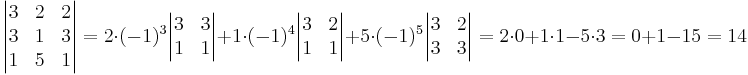
$\begin{vmatrix} 3 & 2 & 2 \\ 3 & 1 & 3 \\ 1 & 5 & 1 \end{vmatrix} = 2 \cdot (-1)^3 \begin{vmatrix} 3 & 3 \\ 1 & 1 \end{vmatrix} + 1 \cdot (-1)^4 \begin{vmatrix} 3 & 2 \\ 1 & 1 \end{vmatrix} + 5 \cdot (-1)^5 \begin{vmatrix} 3 & 2 \\ 3 & 3 \end{vmatrix} = 2 \cdot 0 + 1 \cdot 1 - 5 \cdot 3 = 0 + 1 -15 = 14$

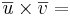
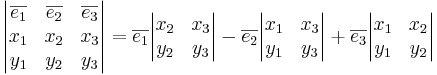
vektorprodukt $\overline{u} \times \overline{v} =$ $\begin{vmatrix} \overline{e_1} & \overline{e_2} & \overline{e_3} \\ x_1 & x_2 & x_3 \\ y_1 & y_2 & y_3 \end{vmatrix} = \overline{e_1} \begin{vmatrix} x_2 & x_3 \\ y_2 & y_3 \end{vmatrix} - \overline{e_2} \begin{vmatrix} x_1 & x_3 \\ y_1 & y_3 \end{vmatrix} + \overline{e_3} \begin{vmatrix} x_1 & x_2 \\ y_1 & y_2 \end{vmatrix}$

[edit] 9.2

Sats4. Om A och B är kvadratiska matriser av samma typ så är det AB = det A $\cdot$ det B

Sats5.

(i) Om A 'r inverterbar så är det 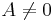$A \neq 0$ och det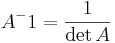 $A^-1 = \frac{1}{\det A}$
(ii) Om A är ortogonal så är det A = 1 eller -1.

[edit] Adjunkten

Med hjälp av underdeterminanter kan man bilda en ny matris.

Definition 3. Med adjunkten till en 3x3 matris menars matrisen:

Adjunkten A = 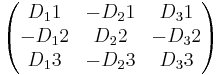$\begin{pmatrix} D_11 & -D_21 & D_31 \\ -D_12 & D_22 & -D_32 \\ D_13 & -D_23 & D_33 \end{pmatrix}$

note Transponering...

För en 2x2 matris gäller det att adj 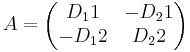$A = \begin{pmatrix} D_11 & -D_21 \\ -D_12 & D_22 \end{pmatrix}$

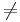Sats: För adjunkmatrisen gäller A $\cdot$ Adj A = Adj A $\cdot$ A = det A $\cdot$ I Om determinanten A $\neq$ 0 så är A inverterbar med inversen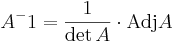 $A^-1 = \frac{1}{\det A} \cdot \mbox{Adj} A$

EX: Bestäm innversen om den existera till 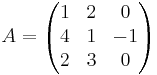$A = \begin{pmatrix} 1 & 2 & 0 \\ 4 & 1 & -1 \\ 2 & 3 & 0 \end{pmatrix}$

det 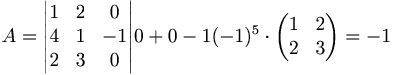$A = \begin{vmatrix} 1 & 2 & 0 \\ 4 & 1 & -1 \\ 2 & 3 & 0 \end{vmatrix} 0 + 0 -1(-1)^5 \cdot \begin{pmatrix} 1 & 2 \\ 2 & 3 \end{pmatrix} = -1$

Eftersom -1 är inte noll, så har matrisen A en invers.

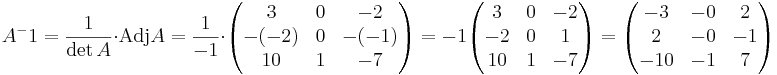
$A^-1 = \frac{1}{\det A} \cdot \mbox{Adj} A = \frac{1}{-1} \cdot \begin{pmatrix} 3 & 0 & -2 \\ -(-2) & 0 & -(-1) \\ 10 & 1 & -7 \end{pmatrix} = -1 \begin{pmatrix} 3 & 0 & -2 \\ -2 & 0 & 1 \\ 10 & 1 & -7 \end{pmatrix} = \begin{pmatrix} -3 & -0 & 2 \\ 2 & -0 & -1 \\ -10 & -1 & 7 \end{pmatrix}$

EX: Beräkna $A - 1$ för 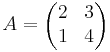$A = \begin{pmatrix} 2 & 3 \\ 1 & 4 \end{pmatrix}$

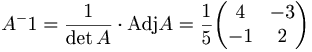
$A^-1 = \frac{1}{\det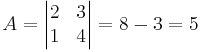 A } \cdot \mbox{Adj} A = \frac{1}{5} \begin{pmatrix} 4 & -3 \\ -1 & 2 \end{pmatrix}$

det $A = \begin{vmatrix} 2 & 3 \\ 1 & 4 \end{vmatrix} = 8 -3 = 5$

EX: Beräkna inversen till 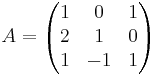$A = \begin{pmatrix} 1 & 0 & 1 \\ 2 & 1 & 0 \\ 1 & -1 & 1 \end{pmatrix}$ Om den existerar.

Det 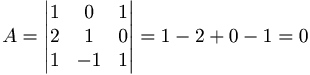$A = \begin{vmatrix} 1 & 0 & 1 \\ 2 & 1 & 0 \\ 1 & -1 & 1 \end{vmatrix} = 1 - 2 + 0 - 1 = 0$

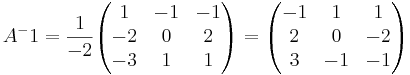
$A^-1 = \frac{1}{-2} \begin{pmatrix} 1 & -1 & -1 \\ -2 & 0 & 2 \\ -3 & 1 & 1 \end{pmatrix} = \begin{pmatrix} -1 & 1 & 1 \\ 2 & 0 & -2 \\ 3 & -1 & -1 \end{pmatrix}$

EX: Beräkna inversen till 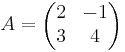$A = \begin{pmatrix} 2 & -1 \\ 3 & 4 \end{pmatrix}$

Det 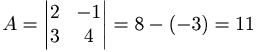$A = \begin{vmatrix} 2 & -1 \\ 3 & 4 \end{vmatrix} = 8 - (-3) = 11$

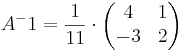
$A^-1 = \frac{1}{11} \cdot \begin{pmatrix} 4 & 1 \\ -3 & 2 \end{pmatrix}$

[edit] 2007-10-12

[edit] Sats 8. Crames regel

Antag att A i AX = Y är av typ 3x3 med det. 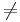$\neq$ 0 då gäller att för varje Y har ekvationsystemet den entydiga lösningen

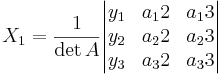
$X_1 = \frac{1}{\det A}\begin{vmatrix} y_1 & a_12 & a_13 \\ y_2 & a_22 & a_23 \\ y_3 & a_32 & a_33 \end{vmatrix}$

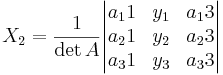
$X_2 = \frac{1}{\det A}\begin{vmatrix} a_11 & y_1 & a_13 \\ a_21 & y_2 & a_23 \\ a_31 & y_3 & a_33 \end{vmatrix}$

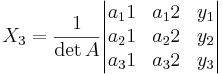
$X_3 = \frac{1}{\det A}\begin{vmatrix} a_11 & a_12 & y_1 \\ a_21 & a_22 & y_2 \\ a_31 & a_32 & y_3 \end{vmatrix}$

Motsvarande gäller om A är kvadratiskt i metris form.

EX: Lös ekvationsystemet

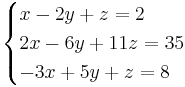
$\begin{cases} x - 2y + z = 2 \\ 2x - 6y + 11z = 35 \\ -3x + 5y + z = 8 \end{cases}$

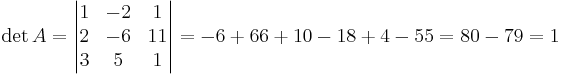
$\det A = \begin{vmatrix} 1 & -2 & 1 \\ 2 & -6 & 11 \\ 3 & 5 & 1 \end{vmatrix} = -6 + 66 + 10 -18 + 4 - 55 = 80 - 79 = 1$

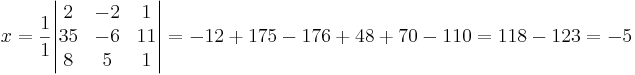
$x = \frac{1}{1} \begin{vmatrix} 2 & -2 & 1 \\ 35 & -6 & 11 \\ 8 & 5 & 1 \end{vmatrix} = -12 + 175 - 176 + 48 + 70 - 110 = 118 - 123 = -5$

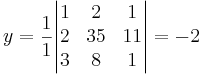
$y = \frac{1}{1} \begin{vmatrix} 1 & 2 & 1 \\ 2 & 35 & 11 \\ 3 & 8 & 1 \end{vmatrix} = -2$

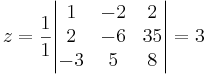
$z = \frac{1}{1} \begin{vmatrix} 1 & -2 & 2 \\ 2 & -6 & 35 \\ -3 & 5 & 8 \end{vmatrix} = 3$

alt: 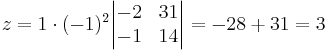$z = 1 \cdot (-1)^2 \begin{vmatrix} -2 & 31 \\ -1 & 14 \end{vmatrix} = -28 + 31 = 3$

[edit] Viktigt: 9.6 Huvudsatsen

Sats 9. För kvadratiska matriser A är följande villkor ekvivalenta:

a) A:s kolonnvektorer är en bas
b) A:s radvektorer är en bas
c) Ekvationsystemet A X = 0 har bara triviala lösningen X = 0
d) Ekvationsystemet A X = Y är lösbart för alla Y
e) A är inverterbar
f) Linjära avbildningar med avbildningsmatrisen A är bijektiva
g) determinanten A 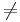$\neq$ 0

Sats 10. För kvadratiska linjära ekvationsystem A X = Y gäller

Homogena system
- Om det A = 0 då finns det inga triviala lösningar
- Om det A 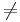$\neq$ 0 då finns det bara triviala lösningar

Inhomogena system
- Om det A = 0 då finns det ingen lösning eller oändligt många
- Om det A 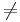$\neq$ 0 då finns det bara entydiga lösningar

Note: homogena system är = 0

[edit] Exempel 1.18: Undersök det inhomogena systemet

Har systemet mer än en lösning för något värde på a?

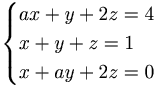
$\begin{cases} ax + y + 2z = 4 \\ x + y + z = 1 \\ x + ay + 2z = 0 \end{cases}$

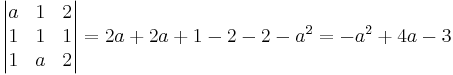
$\begin{vmatrix} a & 1 & 2 \\ 1 & 1 & 1 \\ 1 & a & 2 \end{vmatrix} = 2a + 2a + 1 - 2 - 2 - a^2 = -a^2 + 4a - 3$

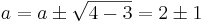
$a = a \pm \sqrt{4-3} = 2 \pm 1$

det A = 0 när a = 3 och a = 1 och då har ekvationsysemet inget lösning eller oändligt många lösningar. Om det 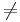$\neq$ 0 när a 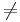$\neq$ 3 och a 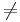$\neq$ 1 då finns entydig lösning.

[edit] Svar:

a = 3 ger: 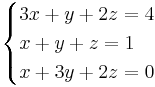$\begin{cases} 3 x + y + 2z = 4 \\ x + y + z = 1 \\ x + 3y + 2z = 0 \end{cases}$

...

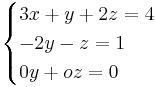
$\begin{cases} 3 x + y + 2z = 4 \\ -2y - z = 1 \\ 0y + oz = 0 \end{cases}$

z = t

Alltså om a = 3 så finns det oändlig antal lösningar!

a = 1 ger: 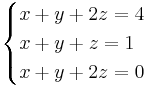$\begin{cases} x + y + 2z = 4 \\ x + y + z = 1 \\ x + y + 2z = 0 \end{cases}$

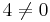
$4 \neq 0$

Om a = 1 så saknas det lösningar

[edit] Exempel 1.17: Lös ekvationsystemet

Lös för varje värde på a ekvationsystemet:

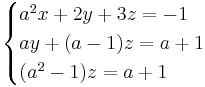
$\begin{cases} a^2x + 2y + 3z = -1 \\ ay + (a-1)z = a + 1 \\ (a^2 - 1)z = a + 1 \end{cases}$

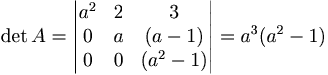
$\det A = \begin{vmatrix} a^2 & 2 & 3 \\ 0 & a & (a-1) \\ 0 & 0 & (a^2 - 1) \end{vmatrix} = a^3 (a^2 - 1)$

$a 3 (a 2 - 1) = 0$

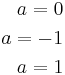
$\begin{align} a = 0 \\ a = -1 \\ a = 1 \end{align}$

[edit] Svar:

a = 0 ger 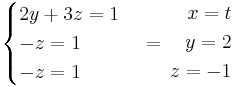$\begin{cases} 2 y + 3z = 1 \\ -z = 1 \\ -z = 1 \end{cases} = \begin{align} x = t \\ y = 2 \\ z = -1 \end{align}$

om a = 0 så finns det oändligt antal lösningar.

a = -1 ger 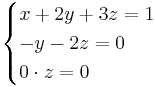$\begin{cases} x + 2 y + 3z = 1 \\ -y -2z = 0 \\ 0 \cdot z = 0 \end{cases}$

$z = t$

om a = -1 så finns det oändligt antal lösningar.

a = 1 ger 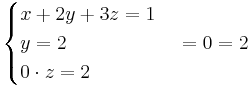$\begin{cases} x +2 y + 3z = 1 \\ y = 2 \\ 0 \cdot z = 2 \end{cases} = 0 = 2$

om a = 1 så saknas det lösning.

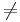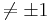för a $\neq$ 0, a $\neq \pm 1$ innebär att det finns entydiga lösningar.

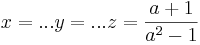
$\begin{align} x = \mbox{...} y = \mbox{...} z = \frac{a+1}{a^2 - 1} \end{align}$

[edit] sats 11. Volymen efter avbildning

Låt F vara en linjär avbildning från rummet till rummet och låt A ara dess avbildningsmatris i någon bas. För godtyckliga vektorer 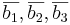$\overline{b_1}, \overline{b_2}, \overline{b_3}$ gäller:

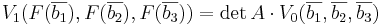
$V_1(F(\overline{b_1}), F(\overline{b_2}), F(\overline{b_3})) = \det A \cdot V_0(\overline{b_1}, \overline{b_2}, \overline{b_3})$

där V_0 är volymen före avbildningen och V_1 är volymen efter avbildning.

Motsvarande gäller för avbildningar från planet till planet.

EX: 5.8 En triangel har hörn i punkterna (1,2,1), (0,4,-1) och (2,0,2).

a) bestäm triangelns area
b) vilken area har triangelns ortogonala projection i xy-planet?

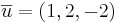
$\overline{u} = (1, 2, -2)$

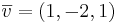
$\overline{v} = (1, -2, 1)$

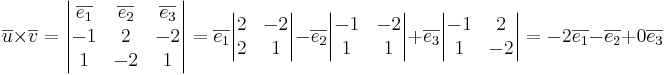
$\overline{u} \times \overline{v} = \begin{vmatrix} \overline{e_1} & \overline{e_2} & \overline{e_3} \\ -1 & 2 & -2 \\ 1 & -2 & 1 \end{vmatrix} = \overline{e_1} \begin{vmatrix} 2 & -2 \\ 2 & 1 \end{vmatrix} - \overline{e_2} \begin{vmatrix} -1 & -2 \\ 1 & 1 \end{vmatrix} + \overline{e_3} \begin{vmatrix} -1 & 2 \\ 1 & -2 \end{vmatrix} = -2\overline{e_1} - \overline{e_2} + 0\overline{e_3}$

Triangelns area är 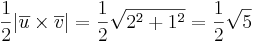$\frac{1}{2} | \overline{u} \times \overline{v} | = \frac{1}{2} \sqrt{2^2 + 1^2} = \frac{1}{2} \sqrt{5}$ a.e.

Avbildningsmatris 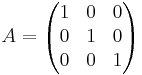$A = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}$

Skalfaktorn = det A. det A = 0.

Ny area 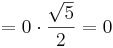$= 0 \cdot \frac{\sqrt{5}}{2} = 0$

[edit] 9.8 Determinanter av högre ordning

Sats 12. motsvarigheten till Satserna 1-11 gäller även allmäna matriser.

För determinanter av större ordning underlättar det om man utvecklar determinantenen efter rad eller kolonn.

EX:

$A = \begin{pmatrix} 2 & 3 & 4 & -1 \\ 1 & -1 & 2 & 0 \\ -2 & 0 & 1 & 1 \\ 2 & 3 & 1 & -1 \end{pmatrix}$

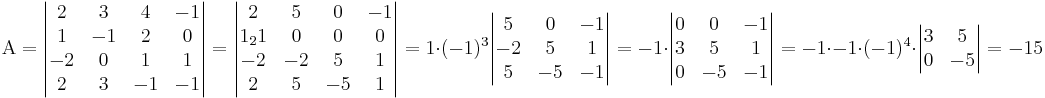
$\mbox{A} = \begin{vmatrix} 2 & 3 & 4 & -1 \\ 1 & -1 & 2 & 0 \\ -2 & 0 & 1 & 1 \\ 2 & 3 & -1 & -1 \end{vmatrix} = \begin{vmatrix} 2 & 5 & 0 & -1 \\ 1_21 & 0 & 0 & 0 \\ -2 & -2 & 5 & 1 \\ 2 & 5 & -5 & 1 \end{vmatrix} = 1 \cdot (-1)^3 \begin{vmatrix} 5 & 0 & -1 \\ -2 & 5 & 1 \\ 5 & -5 & -1 \end{vmatrix} = -1 \cdot \begin{vmatrix} 0 & 0 & -1 \\ 3 & 5 & 1 \\ 0 & -5 & -1 \end{vmatrix} = -1 \cdot -1 \cdot (-1)^4 \cdot \begin{vmatrix} 3 & 5 \\ 0 & -5 \end{vmatrix} = -15$

EX: Beräkna ekvationen för det plan som innehåller punkterna (1,2,3), (1,1,1) och (2,0,1).

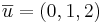
$\overline{u} = (0,1,2)$

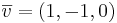
$\overline{v} = (1,-1,0)$

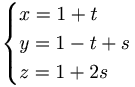
$\begin{cases} x = 1 + t \\ y = 1 - t + s \\ z = 1 + 2s \end{cases}$

Alternativ metod 1:

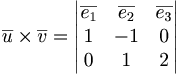
$\overline{u} \times \overline{v} = \begin{vmatrix} \overline{e_1} & \overline{e_2} & \overline{e_3} \\ 1 & -1 & 0 \\ 0 & 1 & 2 \end{vmatrix}$

Alternativ metod 2:

lägg till punkten P:(x,y,z)

vektorn 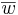$\overline{w}$ blir då:

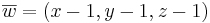
$\overline{w} = (x-1, y-1, z-1)$

det A = 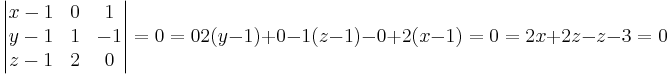$\begin{vmatrix} x-1 & 0 & 1 \\ y-1 & 1 & -1 \\ z-1 & 2 & 0 \end{vmatrix} = 0 = 0 2(y-1) + 0 - 1(z-1) - 0 + 2(x-1) = 0 = 2x + 2z - z -3 = 0$

[edit] Tenta liknade exempel (enkel)

Finns det något värde på konstanten a som gör att ekvationsystemet saknar lösning?

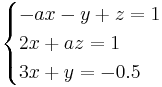
$\begin{cases} -ax - y + z = 1 \\ 2x + az = 1 \\ 3x + y = -0.5 \end{cases}$

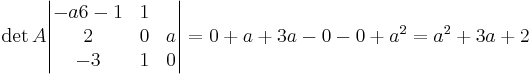
$\det A \begin{vmatrix} -a 6 -1 & 1 \\ 2 & 0 & a \\ -3 & 1 & 0 \end{vmatrix} = 0 + a + 3a - 0 - 0 + a^2 = a^2 + 3a + 2$

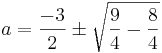
$a = \frac{-3}{2} \pm \sqrt{\frac{9}{4} - \frac{8}{4}}$

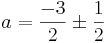
$a = \frac{-3}{2} \pm \frac{1}{2}$

a = -1

a = -2

[edit] Svar

Om a = -1 så:

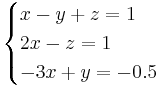
$\begin{cases} x - y + z = 1 \\ 2x - z = 1 \\ -3x + y = -0.5 \end{cases}$

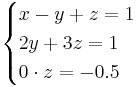
$\begin{cases} x - y +z = 1 \\ 2y + 3z = 1 \\ 0 \cdot z = -0.5 \end{cases}$

Om a = -1 så saknas det lösning

Om a = -2 så:

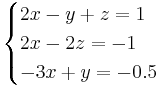
$\begin{cases} 2x - y + z = 1 \\ 2x - 2z = -1 \\ -3x + y = - 0.5 \end{cases}$

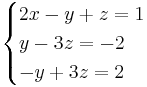
$\begin{cases} 2x - y + z = 1 \\ y - 3z = -2 \\ -y + 3z = 2 \end{cases}$

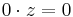
$0 \cdot z = 0$

Alltså om a = -2 så finns det oändligt antal lösningar

[edit] 2. lös matrisekvationen

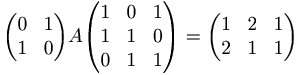
$\begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} A \begin{pmatrix} 1 & 0 & 1 \\ 1 & 1 & 0 \\ 0 & 1 & 1 \end{pmatrix} = \begin{pmatrix} 1 & 2 & 1 \\ 2 & 1 & 1 \end{pmatrix}$

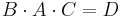
$B \cdot A \cdot C = D$

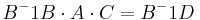
$B^-1 B \cdot A \cdot C = B^-1 D$

$A C C - 1 = B - 1 D C - 1$

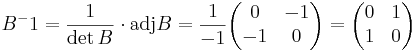
$B^-1 = \frac{1}{\det B} \cdot \mbox{adj} B = \frac{1}{-1} \begin{pmatrix} 0 & -1 \\ -1 & 0 \end{pmatrix} = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}$

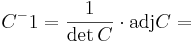
$C^-1 = \frac{1}{\det C} \cdot \mbox{adj} C =$

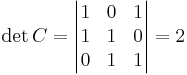
$\det C = \begin{vmatrix} 1 & 0 & 1 \\ 1 & 1 & 0 \\ 0 & 1 & 1 \end{vmatrix} = 2$

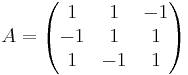
adj $A = \begin{pmatrix} 1 & 1 & -1 \\ -1 & 1 & 1 \\ 1 & -1 & 1 \end{pmatrix}$

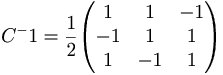
$C^-1 = \frac{1}{2} \begin{pmatrix} 1 & 1 & -1 \\ -1 & 1 & 1 \\ 1 & -1 & 1 \end{pmatrix}$

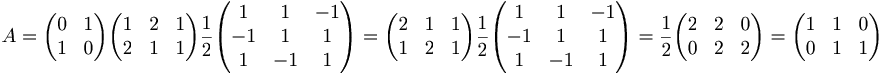
$A = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} \begin{pmatrix} 1 & 2 & 1 \\ 2 & 1 & 1 \end{pmatrix} \frac{1}{2} \begin{pmatrix} 1 & 1 & -1 \\ -1 & 1 & 1 \\ 1 & -1 & 1 \end{pmatrix} = \begin{pmatrix} 2 & 1 & 1 \\ 1 & 2 & 1 \end{pmatrix} \frac{1}{2} \begin{pmatrix} 1 & 1 & -1 \\ -1 & 1 & 1 \\ 1 & -1 & 1 \end{pmatrix} = \frac{1}{2} \begin{pmatrix} 2 & 2 & 0 \\ 0 & 2 & 2 \end{pmatrix} = \begin{pmatrix} 1 & 1 & 0 \\ 0 & 1 & 1 \end{pmatrix}$

[edit] 3. Linjer som skär

Låt $L 1$ vara linen genom punkterna (-2,1,-3) och (-2,3,-2)

$l 2$ är skärningen mellan planen x + 2y + z - y = 0 och 2x + 3y -z -12 = 0. visa att linjera skär varandra och beräkan vinkel mellan dom.

$\begin{cases} x + 2y + z = 7 \cdot [-2]\\ 2x + 3y -z = 12 \end{cases} \to \begin{align} -2x - 4y - 2z = -14 \\ \underline{2x + 3y - z = 12} \\ -y - 3z = -2 \end{align}$

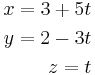
$\begin{align} x = 3 + 5t \\ y = 2 - 3t \\ z = t \end{align}$

$l 1$ har riktningsvektorn 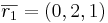$\overline{r_1} = (0,2,1)$

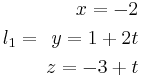
$l_1 = \begin{align} x = -2 \\ y = 1 + 2t \\ z = -3 + t \end{align}$

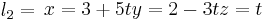
$l_2 = \begin{align} x = 3 + 5t y = 2 - 3t z = t \end{align}$

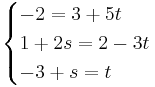
$\begin{cases} -2 = 3 + 5t \\ 1 + 2s = 2 - 3t \\ -3 + s = t \end{cases}$

$5t = 5 \to t = 1$

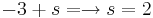
$-3 + s = \to s = 2$

kontrollera i ekv.

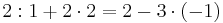
$2: 1 + 2 \cdot 2 = 2 - 3 \cdot (-1)$

$5 = 5$

Alltså linjerna skär varandra i punkten 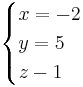$\begin{cases} x = -2 \\ y = 5 \\ z -1 \end{cases}$

$\overline{r_1} \cdot \overline{r_2} = |\overline{r_1}| \cdot |\overline{r_2}| \cdot \cos [\overline{r_1}, \overline{r_2}]$

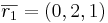
$\overline{r_1} = (0,2,1)$

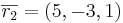
$\overline{r_2} = (5,-3,1)$

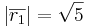
$|\overline{r_1}| = \sqrt{5}$

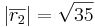
$|\overline{r_2}| = \sqrt{35}$

$(0,2,1)(5,-3,1) = \sqrt{5} \cdot \sqrt{35} \cdot \cos [\overline{r_1}, \overline{r_2}]$

$\cos [\overline{r_1}, \overline{r_2}] = \frac{-5}{\sqrt{5} \sqrt{35}}$

$[\overline{r_1}, \overline{r_2}] = \arccos \frac{-5}{\sqrt{5} \sqrt{35}}$

[edit] 2007-10-19

[edit] Kap 10. Egenvärdeb och egenvektorer

[edit] 10.1 Vad innebär avbildningsmatrisen?

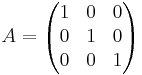
$A = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}$

Denna avbildningsmatris innebär att rummets samtliga punkter projiceras i ett plan tex xy-planet

[edit] 10.2 Definitioner

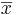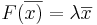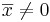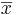Def: Låt F vara en linjär avbildning. Om skalären $λ$ och vektorn $\overline{x}$ uppfyller vilkoret $F(\overline{x)} = \lambda \overline{x}$ med $\overline{x} \neq 0$ sägs $\overline{x}$ är en egenvektor och $λ$ är egenvärde till funktionen F.

Def: Låt A vara en kvadratisk matris. Om skalären $λ$ och kolonnmatrisen X uppfyller $A X = λ X$ där 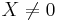$X \neq 0$ sägs X vara egenvektor och $λ$ egenvärde till A.

Bestäm egenvärden och egenvektorer till matrisen 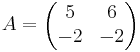$A = \begin{pmatrix} 5 & 6 \\ -2 & -2 \end{pmatrix}$

$A X = λ X$

$A X - λ X = 0$

$(A - λ) X = 0$

Eftersom lambda är ett tal och A en matris, så kan man multiplicera med enhetsmatrisen.

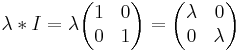
$\lambda * I = \lambda \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} = \begin{pmatrix} \lambda & 0 \\ 0 & \lambda \end{pmatrix}$

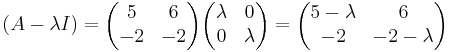
$(A - \lambda I) = \begin{pmatrix} 5 & 6 \\ -2 & -2 \end{pmatrix} \begin{pmatrix} \lambda & 0 \\ 0 & \lambda \end{pmatrix} = \begin{pmatrix} 5 - \lambda & 6 \\ -2 & -2 - \lambda \end{pmatrix}$

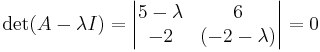
$\det (A - \lambda I) = \begin{vmatrix} 5 - \lambda & 6 \\ -2 & (-2 - \lambda ) \end{vmatrix} = 0$

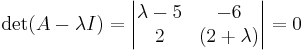
$\det (A - \lambda I) = \begin{vmatrix} \lambda - 5 & -6 \\ 2 & (2 + \lambda ) \end{vmatrix} = 0$

$0 = (λ - 5)(λ + 2) - ( - 12)$

$λ 2 - 3λ - 10 + 12 = 0$

$λ 2 - 3λ + 2 = 0$

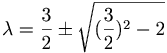
$\lambda = \frac{3}{2} \pm \sqrt{(\frac{3}{2})^2 - 2}$

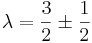
$\lambda = \frac{3}{2} \pm \frac{1}{2}$

$λ 1 = 1$

$λ 2 = 2$

För $λ = 1$ ger:

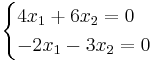
$\begin{cases} 4x_1 + 6x_2 = 0 \\ -2x_1 - 3x_2 = 0 \end{cases}$

$x 1 = - 3 t$

$x 2 = 2 t$

Egenvärdet $λ = 1$ har egenvektorn 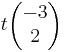$t \begin{pmatrix} -3 \\ 2 \end{pmatrix}$

För $λ = 2$ ger:

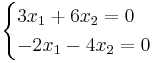
$\begin{cases} 3x_1 + 6x_2 = 0 \\ -2x_1 - 4x_2 = 0 \end{cases}$

$x 1 = - 2 t$

$x 2 = t$

Egenvärdet $λ = 2$ har egenvektorn 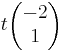$t \begin{pmatrix} -2 \\ 1 \end{pmatrix}$

[edit] 2007-10-24

[edit] Egenvärden

[edit] EX: Bestäm egenvärden och egenvektorer

$det(λ I - A)$

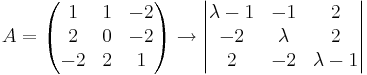
$A = \begin{pmatrix} 1 & 1 & -2 \\ 2 & 0 & -2 \\ -2 & 2 & 1 \end{pmatrix} \to \begin{vmatrix} \lambda -1 & -1 & 2 \\ -2 & \lambda & 2 \\ 2 & -2 & \lambda -1 \end{vmatrix}$

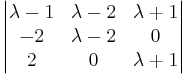
$\begin{vmatrix} \lambda -1 & \lambda -2 & \lambda +1 \\ -2 & \lambda -2 & 0 \\ 2 & 0 & \lambda +1 \end{vmatrix}$

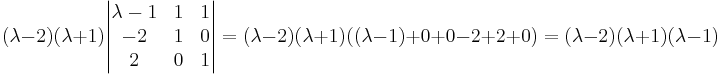
$(\lambda -2 )(\lambda +1) \begin{vmatrix} \lambda -1 & 1 & 1 \\ -2 & 1 & 0 \\ 2 & 0 & 1 \end{vmatrix} = (\lambda -2) (\lambda +1) ((\lambda -1) + 0 + 0 - 2 + 2 + 0) = (\lambda -2)(\lambda +1)(\lambda -1)$

$(λ - 2)(λ + 1)(λ - 1) = 0$

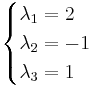
$\begin{cases} \lambda_1 = 2 \\ \lambda_2 = -1 \\ \lambda_3 = 1 \end{cases}$

Beräkna radvis dom 3 nya ekvationerna och sätt indom i ett ekvationsystem

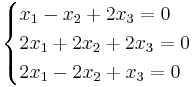
$\begin{cases} x_1 - x_2 + 2x_3 = 0 \\ 2x_1 + 2x_2 + 2x_3 = 0 \\ 2x_1 -2x_2 + x_3 = 0 \end{cases}$

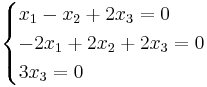
$\begin{cases} x_1 - x_2 + 2x_3 = 0\\ -2x_1 + 2x_2 + 2x_3 = 0 \\ 3x_3 = 0 \end{cases}$

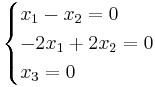
$\begin{cases} x_1 - x_2 = 0\\ -2x_1 + 2x_2 = 0\\ x_3 = 0 \end{cases}$

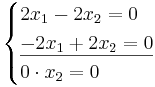
$\begin{cases} 2x_1 - 2x_2 = 0 \\ \underline{-2x_1 + 2x_2 = 0} \\ 0 \cdot x_2 = 0 \end{cases}$

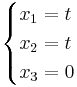
$\begin{cases} x_1 = t \\ x_2 = t \\ x_3 = 0 \end{cases}$

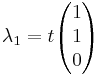
$\lambda_1 = t \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix}$

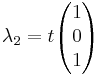
$\lambda_2 = t \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix}$

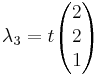
$\lambda_3 = t \begin{pmatrix} 2 \\ 2 \\ 1 \end{pmatrix}$

[edit] Diagnoalisering

Def: Den linjära avbildningen F sägs vara diagonaliserbar om det finns en bas i vilken avbildningsmatrisen för F är en diagonalmatris.

Diagonalmatrisen 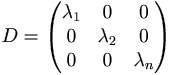$D = \begin{pmatrix} \lambda_1 & 0 & 0 \\ 0 & \lambda_2 & 0 \\ 0 & 0 & \lambda_n \end{pmatrix}$

Def: Matrisen A sägs vara diagonalserbar om det finns en inverterbar matris S och en diagonalmatris D så att $S - 1 A S = D$

Sats: En n x n matris är diagonaliserbar om och endast om det finns n stycken linj. Oberoende egenvektorer till A i formeln $S - 1 A S = D$ är kolonnerna i S egenvektorer till A och diagonalelementen i D är egenvärderna.

Metod för diagonalisering:

(i) Bestäm egenvärden till A
(i) Bestäm egenvektorer till A
(i) Bilda S av egenvektorena
(i) Bilda D av egenvärdena

[edit] EX: Diagonalisera matrisen

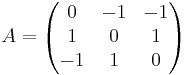
$A = \begin{pmatrix} 0 & -1 & -1 \\ 1 & 0 & 1 \\ -1 & 1 & 0 \end{pmatrix}$

$det(λ I - A) = 0$

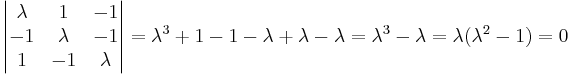
$\begin{vmatrix} \lambda & 1 & -1 \\ -1 & \lambda & -1 \\ 1 & -1 & \lambda \end{vmatrix} = \lambda^3 + 1 - 1 - \lambda + \lambda - \lambda = \lambda^3 - \lambda = \lambda (\lambda^2 - 1) = 0$

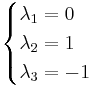
$\begin{cases} \lambda_1 = 0 \\ \lambda_2 = 1 \\ \lambda_3 = -1 \end{cases}$

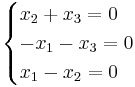
$λ = 0$ ger $\begin{cases} x_2 + x_3 = 0\\ -x_1 - x_3 = 0\\ x_1 - x_2 = 0 \end{cases}$

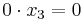
$0 \cdot x_3 = 0$

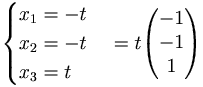
$\begin{cases} x_1 = -t \\ x_2 = -t \\ x_3 = t \end{cases} = t \begin{pmatrix} -1 \\ -1 \\ 1 \end{pmatrix}$

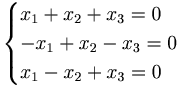
$λ = 1$ ger $\begin{cases} x_1 + x_2 + x_3 = 0\\ -x_1 + x_2 - x_3 = 0\\ x_1 - x_2 + x_3 = 0 \end{cases}$

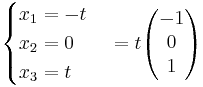
$\begin{cases} x_1 = -t\\ x_2 = 0\\ x_3 = t \end{cases} = t \begin{pmatrix} -1 \\ 0 \\ 1 \end{pmatrix}$

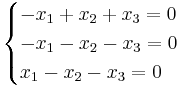
$λ = - 1$ ger $\begin{cases} -x_1 + x_2 + x_3 = 0 \\ -x_1 - x_2 - x_3 = 0 \\ x_1 - x_2 - x_3 = 0 \end{cases}$

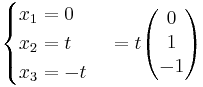
$\begin{cases} x_1 = 0\\ x_2 = t\\ x_3 = -t \end{cases} = t \begin{pmatrix} 0 \\ 1 \\ -1 \end{pmatrix}$

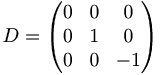
$D = \begin{pmatrix} 0 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & -1 \end{pmatrix}$

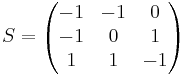
$S = \begin{pmatrix} -1 & -1 & 0 \\ -1 & 0 & 1 \\ 1 & 1 & -1 \end{pmatrix}$

[edit] EX: Beräkna=

$A 5$ om 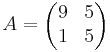$A = \begin{pmatrix} 9 & 5 \\ 1 & 5 \end{pmatrix}$

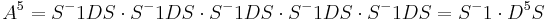
$A^5 = S^-1 D S \cdot S^-1 D S \cdot S^-1 D S \cdot S^-1 D S \cdot S^-1 D S = S^-1 \cdot D^5 S$

$det(λ I - A) = 0$

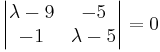
$\begin{vmatrix} \lambda -9 & -5 \\ -1 & \lambda -5 \end{vmatrix} = 0$

$(λ - 9)(λ - 5) - 5 = 0$

$λ 2 - 5λ - 9λ + 45 - 5$

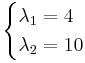
$\begin{cases} \lambda_1 = 4 \\ \lambda_2 = 10 \end{cases}$

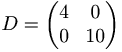
Alltså $D = \begin{pmatrix} 4 & 0 \\ 0 & 10 \end{pmatrix}$

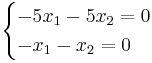
$λ = 4$ ger $\begin{cases} -5 x_1 - 5x_2 = 0 \\ -x_1 - x_2 = 0 \end{cases}$

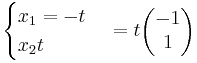
$\begin{cases} x_1 = -t\\ x_2 t \end{cases} = t \begin{pmatrix} -1 \\ 1 \end{pmatrix}$

$λ = 10$ ger $\begin{cases} x_1 - 5x_2 = 0 \\ -x_1 + 5x_2 = 0 \end{cases}$

$\begin{cases} x_1 = 5t\\ x_2 = t \end{cases} = t \begin{pmatrix} 5 \\ 1 \end{pmatrix}$

$S = \begin{pmatrix} -1 & 5 \\ 1 & 1 \end{pmatrix}$

$S^-1 = \frac{1}{-6} \begin{pmatrix} 1 & -5 -1 & -1 \end{pmatrix}$

$A^5 = \frac{1}{6} \begin{pmatrix} -1 & 5 \\ 1 & 1 \end{pmatrix} \begin{pmatrix} 4^5 & 0 \\ 0 & 10^5 \end{pmatrix} \begin{pmatrix} -1 & 5 \\ 1 & 1 \end{pmatrix} = \frac{1}{6} \begin{pmatrix} 4^5 + 5 \cdot 10^5 & 5 \cdot (-4^5)+ 5 \cdot 10^5 \\ -1 \cdot 4^5 + 10^5 & 5 \cdot 4^5 + 10^5 \end{pmatrix}$

MA1106/Lectures

From FUKTwiki

Contents

[edit] Första föreläsningen

[edit] Linjär Algebra

[edit] Gausseliminering

[edit] Vanligt förekommande tentaliknande uppgift

[edit] 2007-09-07

[edit] Allmänt

[edit] Vektormultiplikation

[edit] Subtraktion mellan vektorer

[edit] Baser i planet, rummet och i en linje

[edit] Linjärt beroende eller oberoende

[edit] Example

[edit] 2007-09-12

[edit] Kap 3

[edit] 3.1 kordinatsystem

[edit] 3.2 Linjens Ekvation

[edit] Sammanfattning om linjer

[edit] 3.3 Planets ekvation

[edit] Klassiskt exempel

[edit] Sats 2. Planets ekvation

[edit] 2007-09-14

[edit] Geometrisk teori för linjära ekvationsystem

[edit] Kap4. Skalärprodukt

[edit] Projektionsformlen

[edit] 4.2 Ortonomerad bas

[edit] Vinkelbestämning

[edit] Planets normalriktning

[edit] 2007-09-19

[edit] Avstånds formlen

[edit] Kap 5

[edit] 5.1 Orientering

[edit] 5.2 Vektorproduct och skalär trippleprodukt

[edit] 5.3 räknelagar för vektorprodukt

[edit] 5.4 Vektorprodukt i ortonomerade baser

[edit] 5.5 Några geometriska tillämpningar

[edit] Kvadratiska Linjära ekvationsystem

[edit] 7.5 Invers matris

[edit] 7.6 Matriser och basbyten

[edit] Kap 8 linjära avbildningar

[edit] Funktionsbegreppet

[edit] Matrissambanden

[edit] Hur avbildas en enhetsvektorena?

[edit] 2007-10-05

[edit] Avbildnings vektorer

[edit] Exempel på att skapa en avbildnings vektor

[edit] Svar

[edit] Matriser för speciella avbildningar

[edit] = Matrissamband

[edit] Isometrisk avbildning

[edit] Sammansättning av två funktioner

[edit] EX

[edit] Svar:

[edit] Gammla tenta uppgifter

[edit] Lös ekv.

[edit] Betrakta basbytet:

[edit] SVAR

[edit] Muterad variant

[edit] 2007-10-10

[edit] Kap 9. Determinanter

[edit] 9.1

[edit] 9.2

[edit] Adjunkten

[edit] 2007-10-12

[edit] Sats 8. Crames regel

[edit] Viktigt: 9.6 Huvudsatsen

[edit] Exempel 1.18: Undersök det inhomogena systemet

[edit] Svar:

[edit] Exempel 1.17: Lös ekvationsystemet

[edit] Svar:

[edit] sats 11. Volymen efter avbildning

[edit] 9.8 Determinanter av högre ordning

[edit] Tenta liknade exempel (enkel)

[edit] Svar

[edit] 2. lös matrisekvationen

[edit] 3. Linjer som skär

[edit] 2007-10-19

[edit] Kap 10. Egenvärdeb och egenvektorer

[edit] 10.1 Vad innebär avbildningsmatrisen?