MA1106/Exams

From FUKTwiki

Jump to: navigation, search

Exam solutions made as student notes during lectures and exercises.

[edit] Övnings tenta 2006-01-04

[edit] Uppgift 1. För vilka värden på a

För vilka värden på a har ekvationsystemet en entydig lösning, oändligt antal lösningar och när saknas det lösning?

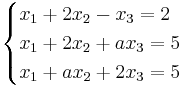
$\begin{cases} x_1 + 2x_2 - x_3 = 2 \\ x_1 + 2x_2 + ax_3 = 5\\ x_1 + ax_2 + 2x_3 = 5 \end{cases}$

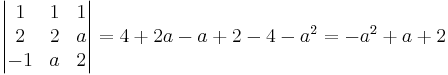
$\begin{vmatrix} 1 & 1 & 1 \\ 2 & 2 & a \\ -1 & a & 2 \end{vmatrix} = 4 + 2a - a + 2 - 4 - a^2 = -a^2 + a + 2$

$a 2 - a - 2 = 0$

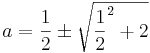
$a = \frac{1}{2} \pm \sqrt{\frac{1}{2}^2 + 2}$

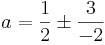
$a = \frac{1}{2} \pm \frac{3}{-2}$

$a 1 = 2$

$a 2$

[edit] a = 2 ger

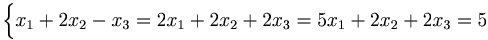
$\begin{cases} x_1 + 2x_2 - x_3 = 2 x_1 + 2x_2 + 2x_3 = 5 x_1 + 2x_2 + 2x_3 = 5 \end{cases}$

ekvation 1 och 2 ger : $0 x 1 + 0 x 2 + 3 x 3 = 3$

$x 3 = 1$

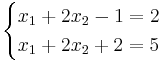
$\begin{cases} x_1 + 2x_2 - 1 = 2 \\ x_1 + 2x_2 + 2 = 5 \end{cases}$

$x 2 = t$

alltså oändligt antal lösningar

[edit] a = -1 ger

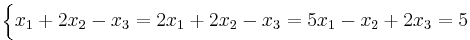
$\begin{cases} x_1 + 2x_2 - x_3 = 2 x_1 + 2x_2 -x_3 = 5 x_1 - x_2 + 2x_3 = 5 \end{cases}$

Ekvation 1 och 2 get : $0 = 3$

alltså så saknas det lösning

[edit] Svar:

Om a = 2 så har vi oändligt antal lösningar.

Om a = -1 saknar vi lösning

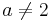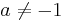Om $a \neq 2$ och $a \neq -1$ så finns det entydiga lösningar

[edit] Uppgift 2 a). Lös matrisekvationen

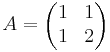
$A = \begin{pmatrix} 1 & 1 \\ 1 & 2 \end{pmatrix}$

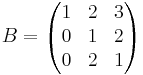
$B = \begin{pmatrix} 1 & 2 & 3 \\ 0 & 1 & 2 \\ 0 & 2 & 1 \end{pmatrix}$

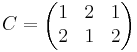
$C = \begin{pmatrix} 1 & 2 & 1 \\ 2 & 1 & 2 \end{pmatrix}$

$A X B = C$

$A - 1 A X B B - 1 = A - 1 C B - 1$

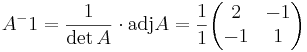
$A^-1 = \frac{1}{\det A} \cdot \mbox{adj} A = \frac{1}{1} \begin{pmatrix} 2 & -1 \\ -1 & 1 \end{pmatrix}$

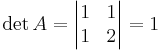
$\det A = \begin{vmatrix} 1 & 1 \\ 1 & 2 \end{vmatrix} = 1$

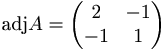
$\mbox{adj} A = \begin{pmatrix} 2 & -1 \\ -1 & 1 \end{pmatrix}$

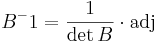
$B^-1 = \frac{1}{\det B} \cdot \mbox{adj}$

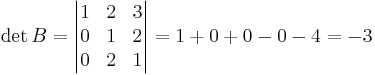
$\det B = \begin{vmatrix} 1 & 2 & 3 \\ 0 & 1 & 2 \\ 0 & 2 & 1 \end{vmatrix} = 1 + 0 + 0 - 0 - 4 = -3$

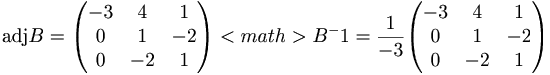
$\mbox{adj} B = \begin{pmatrix} -3 & 4 & 1 \\ 0 & 1 & -2 \\ 0 & -2 & 1 \end{pmatrix} <math>B^-1 = \frac{1}{-3} \begin{pmatrix} -3 & 4 & 1 \\ 0 & 1 & -2 \\ 0 & -2 & 1 \end{pmatrix}$

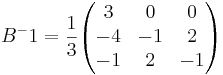
$B^-1 = \frac{1}{3} \begin{pmatrix} 3 & 0 & 0 \\ -4 & -1 & 2 \\ -1 & 2 & -1 \end{pmatrix}$

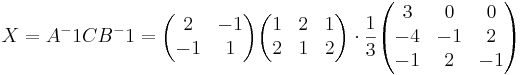
$X = A^-1 C B^-1 = \begin{pmatrix} 2 & -1 \\ -1 & 1 \end{pmatrix} \begin{pmatrix} 1 & 2 & 1 \\ 2 & 1 & 2 \end{pmatrix} \cdot \frac{1}{3} \begin{pmatrix} 3 & 0 & 0 \\ -4 & -1 & 2 \\ -1 & 2 & -1 \end{pmatrix}$

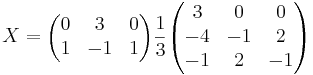
$X = \begin{pmatrix} 0 & 3 & 0 \\ 1 & -1 & 1 \end{pmatrix} \frac{1}{3} \begin{pmatrix} 3 & 0 & 0 \\ -4 & -1 & 2 \\ -1 & 2 & -1 \end{pmatrix}$

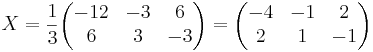
$X = \frac{1}{3} \begin{pmatrix} -12 & -3 & 6 \\ 6 & 3 & -3 \end{pmatrix} = \begin{pmatrix} -4 & -1 & 2 \\ 2 & 1 & -1 \end{pmatrix}$

[edit] Svar:

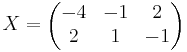
$X = \begin{pmatrix} -4 & -1 & 2 \\ 2 & 1 & -1 \end{pmatrix}$

[edit] Uppgift 2 a). För vilka r är matrisen A inverterbar

Antag att 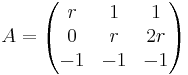$A = \begin{pmatrix} r & 1 & 1 \\ 0 & r & 2r \\ -1 & -1 & -1 \end{pmatrix}$

För vilka är matrisen A inverterbar

När $det A$ är skild från noll.

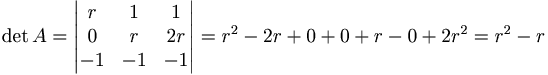
$\det A = \begin{vmatrix} r & 1 & 1 \\ 0 & r & 2r \\ -1 & -1 & -1 \end{vmatrix} = r^2 - 2r + 0 + 0 + r - 0 + 2r^2 = r^2 - r$

$r (r - 1) = 0$

$r 1 = 0$

$r 2 = 1$

[edit] Svar:

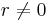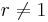Om $r \neq 0$ och $r \neq 1$ är matrisen inverterbar.

[edit] Uppgift 3. Beräkna kortaste avståndet

Beräkna det kortaste avståndet mellan linjerna

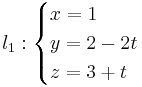
$l_1 : \begin{cases} x = 1 \\ y = 2 - 2t \\ z = 3 + t \end{cases}$

$l 2 :(x, y, z) = (1,2,0) + t (4, - 3,1)$

Ta fram en vektor som är vinkelrät mot båda linjerna.

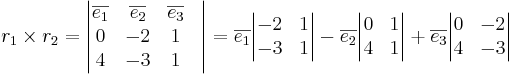
$r_1 \times r_2 = \begin{vmatrix} \overline{e_1} & \overline{e_2} & \overline{e_3} \\ 0 & -2 & 1 & \\ 4 & -3 & 1 & \end{vmatrix} = \overline{e_1} \begin{vmatrix} -2 & 1 \\ -3 & 1 \end{vmatrix} - \overline{e_2} \begin{vmatrix} 0 & 1 \\ 4 & 1 \end{vmatrix} + \overline{e_3} \begin{vmatrix} 0 & -2 \\ 4 & -3 \end{vmatrix}$

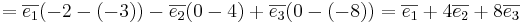
$= \overline{e_1} (-2-(-3)) - \overline{e_2} (0-4) + \overline{e_3} (0-(-8)) = \overline{e_1} + 4 \overline{e_2} + 8 \overline{e_3}$

alltså $\overline{r_1} \times \overline{r_2} = (1,4,8)$

$P 1 :(1,2,3)$

$P 2 :(1,2,0)$

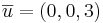
$\overline{u} = (0,0,3)$

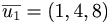
$\overline{u_1} = (1,4,8)$

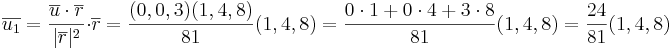
$\overline{u_1} = \frac{\overline{u} \cdot \overline{r}}{|\overline{r}|^2} \cdot \overline{r} = \frac{(0,0,3)(1,4,8)}{81} (1,4,8) = \frac{0\cdot 1 + 0 \cdot 4 + 3 \cdot 8}{81}(1,4,8) = \frac{24}{81} (1,4,8)$

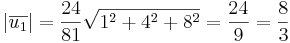
$|\overline{u_1}| = \frac{24}{81} \sqrt{1^2 + 4^2 + 8^2} = \frac{24}{9} = \frac{8}{3}$

[edit] Svar:

Alltså 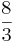$\frac{8}{3}$ l.e.

[edit] Uppgift 4 a). Visa att vektorena är linjärt oberoende

Antag att 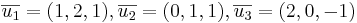$\overline{u_1} = (1,2,1), \overline{u_2} = (0,1,1), \overline{u_3} = (2,0,-1)$

Visa att vektorena 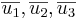$\overline{u_1}, \overline{u_2}, \overline{u_3}$ utgör en bas i $R 3$ dvs att vektorena 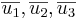$\overline{u_1}, \overline{u_2}, \overline{u_3}$ är linjärt oberoende.

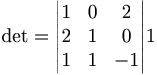
$\det = \begin{vmatrix} 1 & 0 & 2 \\ 2 & 1 & 0 \\ 1 & 1 & -1 \end{vmatrix} 1$

om 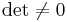$\det \neq 0$ så är dom linjärt oberoende

[edit] Svar:

alltså 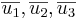$\overline{u_1}, \overline{u_2}, \overline{u_3}$ är linjärt oberoende och utgör en bas i $R 3$

[edit] Uppgift 4 b). Bestäm koordinaterna med avseende på basen

Antag att 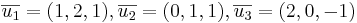$\overline{u_1} = (1,2,1), \overline{u_2} = (0,1,1), \overline{u_3} = (2,0,-1)$

Bestäm koordinaterna för vektorn (0,3,0) med avseende på basen 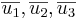$\overline{u_1}, \overline{u_2}, \overline{u_3}$

$u$ = (0,3,0)

Basbytematris 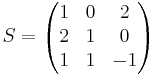$S = \begin{pmatrix} 1 & 0 & 2 \\ 2 & 1 & 0 \\ 1 & 1 & -1 \end{pmatrix}$

X = S X'

X' = $S - 1$ X

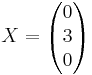
$X = \begin{pmatrix} 0 \\ 3 \\ 0 \end{pmatrix}$

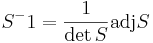
$S^-1 = \frac{1}{\det S} \mbox{adj} S$

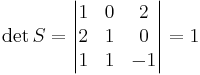
$\det S = \begin{vmatrix} 1 & 0 & 2 \\ 2 & 1 & 0 \\ 1 & 1 & -1 \end{vmatrix} = 1$

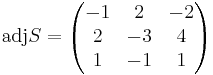
$\mbox{adj} S = \begin{pmatrix} -1 & 2 & -2 \\ 2 & -3 & 4 \\ 1 & -1 & 1 \end{pmatrix}$

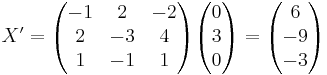
$X' = \begin{pmatrix} -1 & 2 & -2 \\ 2 & -3 & 4 \\ 1 & -1 & 1 \end{pmatrix} \begin{pmatrix} 0 \\ 3 \\ 0 \end{pmatrix} = \begin{pmatrix} 6 \\ -9 \\ -3 \end{pmatrix}$

[edit] Svar:

vektorn 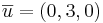$\overline{u} = (0,3,0)$ får koordinaterna $(6, - 9, - 3)$ i den nya basen

[edit] Uppgift 5. Beräkna avståndet mellan linje och punkt

Linjen l ges av skärningen mellan planen x - 2y + 3z = -1 och x + y - 6z = 0. beräkna det kortaste avståndet mellan punkten P (1,-1,0) och linjen l.

hint : Beräkna linjen. hitta på en godtycklig punkt på linjen, beräkna vektorn. Projecera den nya vektorn på linjen. Minska den nya projecerade linjen med den beräknade vetkorn.

$\begin{cases} x - 2y + 3z = 1 [-1]\\ x + y - 6z = 0 \end{cases} \to \begin{align} -x + 2y - 3z = 1 \\ \underline{x + y - 6z = 0} 3y - 9z = 1 \end{align}$

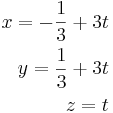
$\begin{align} x = - \frac{1}{3} + 3t \\ y = \frac{1}{3} + 3t \\ z = t \end{align}$

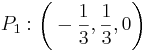
$P_1 : \biggl( -\frac{1}{3}, \frac{1}{3}, 0 \biggr)$

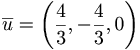
$\overline{u} = \biggl( \frac{4}{3}, -\frac{4}{3}, 0 \biggr)$

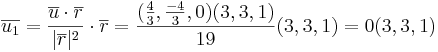
$\overline{u_1} = \frac{\overline{u} \cdot \overline{r}}{|\overline{r}|^2} \cdot \overline{r} = \frac{(\frac{4}{3}, \frac{-4}{3}, 0)(3,3,1)}{19} (3,3,1) = 0 (3,3,1)$

[edit] Svar:

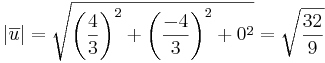
$|\overline{u}| = \sqrt{ \biggl( \frac{4}{3} \biggr) ^2 + \biggl( \frac{-4}{3} \biggr) ^2 + 0^2} = \sqrt{\frac{32}{9}}$

[edit] Uppgift 6. Ange avbildningsmatrisen

Ange avbildningsmatrisen för den linjära avbildning som består i att man först rotera rummets vektorer vinkeln 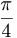$\frac{\pi}{4}$ runt y-axeln (moturs i y-axelns positiva riktning) och därefter speglar rummets vektorer i linjen (x,y,z) = t(1,1,0)

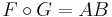
$F \circ G = A B$

G är det man gör först med avbildningsmatrise B.

F har avbildningsmatrisen A.

Börjar med att kontrollera vad sm händer med enhetsvektorena

Rotation 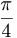$\frac{\pi}{4}$

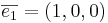$\overline{e_1} = (1,0,0)$ får koordinaterna $(\frac{1}{\sqrt{2}}, 0, - \frac{1}{\sqrt{2}})$

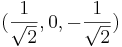
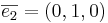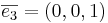$\overline{e_2} = (0,1,0)$ får koordinaterna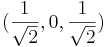 $(0,1,0)$

$\overline{e_3} = (0,0,1)$ får koordinaterna $(\frac{1}{\sqrt{2}}, 0, \frac{1}{\sqrt{2}})$

Avbildningsmatrisen 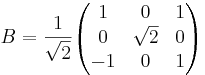$B = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 & 0 & 1 \\ 0 & \sqrt{2} & 0 \\ -1 & 0 & 1 \end{pmatrix}$

Spegling

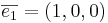$\overline{e_1} = (1,0,0)$ får koordinaterna (0,1,0)

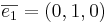$\overline{e_1} = (0,1,0)$ får koordinaterna (1,0,0)

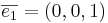$\overline{e_1} = (0,0,1)$ får koordinaterna (0,0,-1)

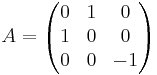
$A = \begin{pmatrix} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 &-1 \end{pmatrix}$

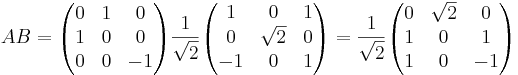
$A B = \begin{pmatrix} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & -1 \end{pmatrix} \frac{1}{\sqrt{2}} \begin{pmatrix} 1 & 0 & 1 \\ 0 & \sqrt{2} & 0 \\ -1 & 0 & 1 \end{pmatrix} = \frac{1}{\sqrt{2}} \begin{pmatrix} 0 & \sqrt{2} & 0 \\ 1 & 0 & 1 \\ 1 & 0 & -1 \end{pmatrix}$

[edit] Svar:

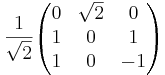
$\frac{1}{\sqrt{2}} \begin{pmatrix} 0 & \sqrt{2} & 0 \\ 1 & 0 & 1 \\ 1 & 0 & -1 \end{pmatrix}$

[edit] Övningstenta 2007-06-04

[edit] Uppgift 1. Bestäm lösningen till ekvationssystemet

Bestäm hur lösningen till ekvationssystemet beror på värdet på a.

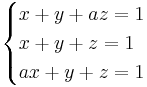
$\begin{cases} x + y + az = 1 \\ x + y + z = 1 \\ ax + y + z = 1 \end{cases}$

Beräkna när determinanten Är skild från 0.

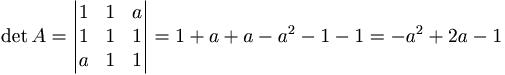
$\det A = \begin{vmatrix} 1 & 1 & a \\ 1 & 1 & 1 \\ a & 1 & 1 \end{vmatrix} = 1 + a + a - a^2 - 1 - 1 = -a^2 + 2 a - 1$

$a 2 - 2 a + 1 = 0$

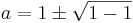
$a = 1 \pm \sqrt{1 - 1}$

$a = 1$ ger:

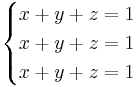
$\begin{cases} x + y + z = 1 \\ x + y + z = 1 \\ x + y + z = 1 \end{cases}$

oändligt antal lösningar.

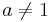$a \neq 1$ ger:

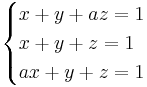
$\begin{cases} x + y + az = 1 \\ x + y + z = 1 \\ ax + y + z = 1 \end{cases}$

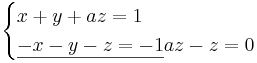
$\begin{cases} x + y + az = 1 \\ \underline{-x - y - z = -1} az - z = 0 \end{cases}$

$(a - 1) z = 0$

slutsats: z måste vara 0 om 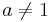$a \neq 1$ .

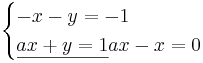
$\begin{cases} -x - y = -1 \\ \underline{ax + y = 1} ax - x = 0 \end{cases}$

slutsats: x måste vara 0 om 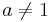$a \neq 1$ och då måste y vara lika med 1.

[edit] Svar:

Alltså oändligt antal många lösningar om a = 1. Om a 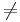$\neq$ 1 så finns det entydiga lösningar.

för dom entydiga lösningarna måste:

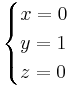
$\begin{cases} x = 0 \\ y = 1 \\ z = 0 \end{cases}$

[edit] Uppgift 2 a): Bestäm arean av triangeln

Bestäm arean av en triangel med hörn i punkterna (1,2,3), (3,1,2) och (-4,0,4)

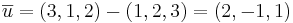
$\overline{u} = (3,1,2)-(1,2,3) = (2,-1,1)$

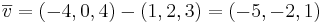
$\overline{v} = (-4,0,4) - (1,2,3) = (-5, -2, 1)$

Arean av triangeln är 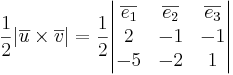$\frac{1}{2} |\overline{u} \times \overline{v}| = \frac{1}{2} \begin{vmatrix} \overline{e_1} & \overline{e_2} & \overline{e_3} \\ 2 & -1 & -1 \\ -5 & -2 & 1 \end{vmatrix}$

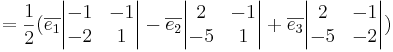
$= \frac{1}{2} ( \overline{e_1} \begin{vmatrix} -1 & -1 \\ -2 & 1 \end{vmatrix} - \overline{e_2} \begin{vmatrix} 2 & -1 \\ -5 & 1 \end{vmatrix} + \overline{e_3} \begin{vmatrix} 2 & -1 \\ -5 & -2 \end{vmatrix} )$

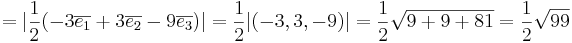$= | \frac{1}{2} ( -3\overline{e_1} + 3 \overline{e_2} - 9 \overline{e_3})| = \frac{1}{2} | (-3,3,-9)| = \frac{1}{2} \sqrt{9+9+81} = \frac{1}{2} \sqrt{99}$ a.e

[edit] Svar:

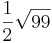
$\frac{1}{2} \sqrt{99}$

[edit] Uppgift 2 b): Beräkna volymen

Beräkna volymen av en parallellepiped som späns upp av vektorena 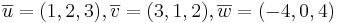$\overline{u} = (1,2,3), \overline{v} = (3,1,2), \overline{w} = (-4,0,4)$

Volymen av en parallellepiped är lika med determinantens belopp.

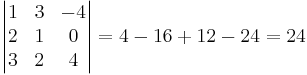
$\begin{vmatrix} 1 & 3 & -4 \\ 2 & 1 & 0 \\ 3 & 2 & 4 \end{vmatrix} = 4 -16 + 12 -24 = 24$

alltså volymen är 24 v.e

[edit] Lös matrisekvationen

Lös matrisekvationen A X B = C

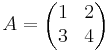
$A = \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix}$

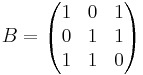
$B = \begin{pmatrix} 1 & 0 & 1 \\ 0 & 1 & 1 \\ 1 & 1 & 0 \end{pmatrix}$

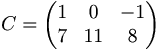
$C = \begin{pmatrix} 1 & 0 & -1 \\ 7 & 11 & 8 \end{pmatrix}$

$A - 1 A X B B - 1 = A - 1 C B - 1$

$X = A - 1 C B - 1$

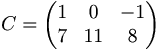
$C = \begin{pmatrix} 1 & 0 & -1 \\ 7 & 11 & 8 \end{pmatrix}$

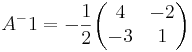
$A^-1 = - \frac{1}{2} \begin{pmatrix} 4 & -2 \\ -3 & 1 \end{pmatrix}$

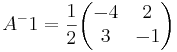
$A^-1 = \frac{1}{2} \begin{pmatrix} -4 & 2 \\ 3 & -1 \end{pmatrix}$

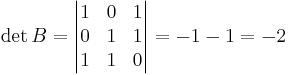
$\det B = \begin{vmatrix} 1 & 0 & 1 \\ 0 & 1 & 1 \\ 1 & 1 & 0 \end{vmatrix} = -1 - 1 = -2$

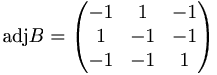
$\mbox{adj} B = \begin{pmatrix} -1 & 1 & -1 \\ 1 & -1 & -1 \\ -1 & -1 & 1 \end{pmatrix}$

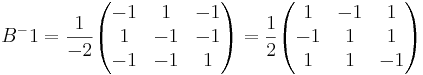
$B^-1 = \frac{1}{-2} \begin{pmatrix} -1 & 1 & -1 \\ 1 & -1 & -1 \\ -1 & -1 & 1 \end{pmatrix} = \frac{1}{2} \begin{pmatrix} 1 & -1 & 1 \\ -1 & 1 & 1 \\ 1 & 1 & -1 \end{pmatrix}$

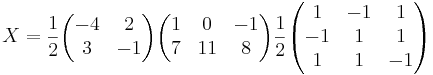
$X = \frac{1}{2} \begin{pmatrix} -4 & 2 \\ 3 & -1 \end{pmatrix} \begin{pmatrix} 1 & 0 & -1 \\ 7 & 11 & 8 \end{pmatrix} \frac{1}{2} \begin{pmatrix} 1 & -1 & 1 \\ -1 & 1 & 1 \\ 1 & 1 & -1 \end{pmatrix}$

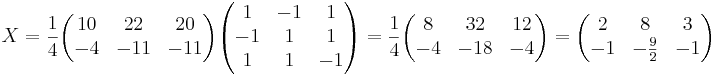
$X = \frac{1}{4} \begin{pmatrix} 10 & 22 & 20 \\ -4 & -11 & -11 \end{pmatrix} \begin{pmatrix} 1 & -1 & 1 \\ -1 & 1 & 1 \\ 1 & 1 & -1 \end{pmatrix} = \frac{1}{4} \begin{pmatrix} 8 & 32 & 12 \\ -4 & -18 & -4 \end{pmatrix} = \begin{pmatrix} 2 & 8 & 3 \\ -1 & - \frac{9}{2} & -1 \end{pmatrix}$

[edit] Uppgift 4 a): Linjärt oberoende?

Visa att vektorena 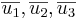$\overline{u_1}, \overline{u_2}, \overline{u_3}$ ugör en bas i $R 3$ dvs, att vektorena 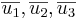$\overline{u_1}, \overline{u_2}, \overline{u_3}$ är linjärt oberoende.

Om determinaten är skild från noll så är dom linjärt oberoende.

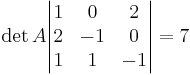
$\det A \begin{vmatrix} 1 & 0 & 2 \\ 2 & -1 & 0 \\ 1 & 1 & -1 \end{vmatrix} = 7$

[edit] Svar:

Determinaten är 7 dvs inte noll, så dom är linjärt oberoende och därmed utgör en bas i $R 3$ .

[edit] Uppgift 4 b): Bestäm koordinaterna för vektorn

Bestäm koordinaterna för vektorn (0,7,0) med avseende på basen 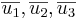$\overline{u_1}, \overline{u_2}, \overline{u_3}$

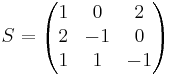
$S = \begin{pmatrix} 1 & 0 & 2 \\ 2 & -1 & 0 \\ 1 & 1 & -1 \end{pmatrix}$

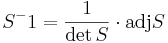
$S^-1 = \frac{1}{\det S} \cdot \mbox{adj} S$

$det S = 7$

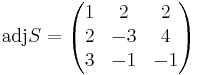
$\mbox{adj} S = \begin{pmatrix} 1 & 2 & 2 \\ 2 & -3 & 4 \\ 3 & -1 & -1 \end{pmatrix}$

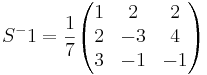
$S^-1 = \frac{1}{7} \begin{pmatrix} 1 & 2 & 2 \\ 2 & -3 & 4 \\ 3 & -1 & -1 \end{pmatrix}$

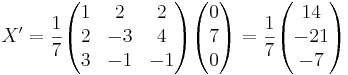
$X' = \frac{1}{7} \begin{pmatrix} 1 & 2 & 2 \\ 2 & -3 & 4 \\ 3 & -1 & -1 \end{pmatrix} \begin{pmatrix} 0 \\ 7 \\ 0 \end{pmatrix} = \frac{1}{7} \begin{pmatrix} 14 \\ -21 \\ -7 \end{pmatrix}$

[edit] Svar:

Den nya vektorn får koordinaterna (2,-3,-1)

[edit] Uppgift 5: Koordinaterna för linjen

Ange ekvationen för den räta linjen, som går genom punkten P (4,0,0) och under rät vinkel skär linjen 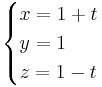$\begin{cases} x = 1 + t \\ y = 1 \\ z = 1 - t \end{cases}$

Ta den godtyckliga punkten (1,1,1) från linjen och beräkan vektorn mellan den nya punkten och P.

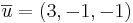
$\overline{u} = (3,-1,-1)$

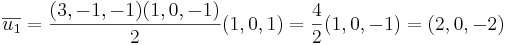
$\overline{u_1} = \frac{(3,-1,-1)(1,0,-1)}{2} (1,0,1) = \frac{4}{2} (1,0,-1) = (2,0,-2)$

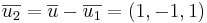
$\overline{u_2} = \overline{u} - \overline{u_1} = (1,-1, 1)$

$L :(4,0,0) + t (1, - 1,1)$

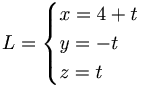
$L = \begin{cases} x = 4 + t \\ y = -t \\ z = t \end{cases}$

[edit] Svar:

Den nya linjen blir (4,0,0) + t(1,-1,1)

[edit] Uppgift 6: Spegling och vridning

Låt F vara den linjära avbildning som speglar rummets vektorer i planet $x 1 - 2 x 2 + 2 x 3 = 0$ , och låt G vara den linjära avbildning som vridet rummets vektorer med vinkeln 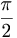$\frac{\pi}{2}$ i positiv riktning kring $x 3$ - axlen (z - axlen).

[edit] A) bestäm matrisen till F

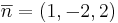
$\overline{n} = (1, -2, 2)$

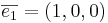
$\overline{e_1} = (1,0,0)$

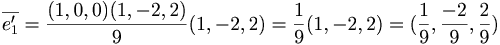
$\overline{e_1'} = \frac{(1,0,0)(1,-2,2)}{9} (1,-2,2) = \frac{1}{9} (1,-2,2) = (\frac{1}{9}, \frac{-2}{9}, \frac{2}{9})$

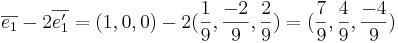
$\overline{e_1} - 2 \overline{e_1'} = (1,0,0) - 2(\frac{1}{9}, \frac{-2}{9}, \frac{2}{9}) = (\frac{7}{9}, \frac{4}{9}, \frac{-4}{9})$

Bestäm A. 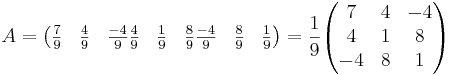$A = \begin{pmatrix} \frac{7}{9} & \frac{4}{9} & \frac{-4}{9} \frac{4}{9} & \frac{1}{9} & \frac{8}{9} \frac{-4}{9} & \frac{8}{9} & \frac{1}{9} \end{pmatrix} = \frac{1}{9} \begin{pmatrix} 7 & 4 & -4 \\ 4 & 1 & 8 \\ -4 & 8 & 1 \end{pmatrix}$

$(1,0,0) + t (1, - 2,2) = (1 + t, - 2 t,2 t)$ , slå ihop det med planets ekvation

$1 + t - 2( - 2 t) + 2(2 t) = 1 + 9 t$

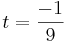
$t = \frac{-1}{9}$

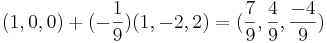
$(1,0,0) + (-\frac{1}{9})(1,-2,2) = (\frac{7}{9}, \frac{4}{9}, \frac{-4}{9})$

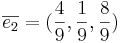
$\overline{e_2} = (\frac{4}{9}, \frac{1}{9}, \frac{8}{9})$

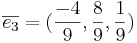
$\overline{e_3} = (\frac{-4}{9}, \frac{8}{9}, \frac{1}{9})$

[edit] b)

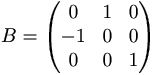
$B = \begin{pmatrix} 0 & 1 & 0 \\ -1 & 0 & 0 \\ 0 & 0 & 1 \end{pmatrix}$

[edit] C)

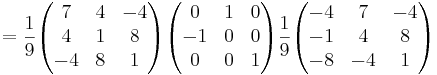
$= \frac{1}{9} \begin{pmatrix} 7 & 4 & -4 \\ 4 & 1 & 8 \\ -4 & 8 & 1 \end{pmatrix} \begin{pmatrix} 0 & 1 & 0 \\ -1 & 0 & 0 \\ 0 & 0 & 1 \end{pmatrix} \frac{1}{9} \begin{pmatrix} -4 & 7 & -4 \\ -1 & 4 & 8 \\ -8 & -4 & 1 \end{pmatrix}$

[edit] Övnings tenta 2002-03-12

[edit] Uppgift 1 Lös ekvationsystemet

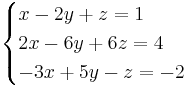
$\begin{cases} x - 2y + z = 1 \\ 2x - 6y + 6z = 4 \\ -3x + 5y - z = -2 \end{cases}$

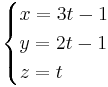
$\begin{cases} x = 3t -1 \\ y = 2t - 1 \\ z = t \end{cases}$

[edit] Uppgift 2 bestäm matrisen X

Bestäm matrisen X i ekvationen $A X + B T = C$

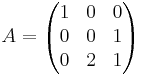
$A = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 2 & 1 \end{pmatrix}$

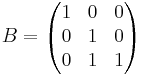
$B = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 1 & 1 \end{pmatrix}$

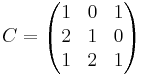
$C = \begin{pmatrix} 1 & 0 & 1 \\ 2 & 1 & 0 \\ 1 & 2 & 1 \end{pmatrix}$

$A X + B T = C$

$A X = C - B T$

$A - 1 A X = A - 1(C - B T)$

$X = A - 1(C - B T)$

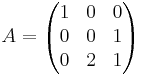
$A = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 2 & 1 \end{pmatrix}$

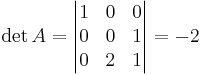
$\det A = \begin{vmatrix} 1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 2 & 1 \end{vmatrix} = -2$

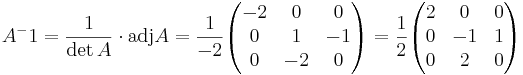
$A^-1 = \frac{1}{\det A} \cdot \mbox{adj} A = \frac{1}{-2} \begin{pmatrix} -2 & 0 & 0\\ 0 & 1 & -1\\ 0 & -2 & 0 \end{pmatrix} = \frac{1}{2} \begin{pmatrix} 2 & 0 & 0\\ 0 & -1 & 1\\ 0 & 2 & 0 \end{pmatrix}$

Kontroll:

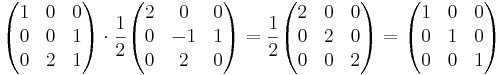
$\begin{pmatrix} 1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 2 & 1 \end{pmatrix} \cdot \frac{1}{2} \begin{pmatrix} 2 & 0 & 0\\ 0 & -1 & 1\\ 0 & 2 & 0 \end{pmatrix} = \frac{1}{2} \begin{pmatrix} 2 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 2 \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}$

då har vi bevisat att den är rätt.

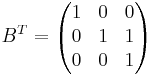
$B^T = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 1 \\ 0 & 0 & 1 \end{pmatrix}$

note $B T$ är kolummer skrivna som rader

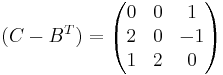
$(C - B^T) = \begin{pmatrix} 0 & 0 & 1 \\ 2 & 0 & -1 \\ 1 & 2 & 0 \end{pmatrix}$

$X = \frac{1}{2} \begin{pmatrix} 2 & 0 & 0\\ 0 & -1 & 1\\ 0 & 2 & 0 \end{pmatrix} \begin{pmatrix} 0 & 0 & 1 \\ 2 & 0 & -1 \\ 1 & 2 & 0 \end{pmatrix} = \frac{1}{2} \begin{pmatrix} 0 & 0 & 2 \\ -1 & 2 & 1 \\ 4 & 0 & -2 \end{pmatrix}$

[edit] Uppgift 3: En triangel

En triangel har hörn i punkterna (1,2,3), (1,1,1) och (2,0,1)

[edit] a) Bestäm arean

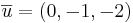
$\overline{u} = (0,-1,-2)$

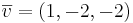
$\overline{v} = (1,-2,-2)$

Triangelns area är 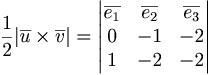$\frac{1}{2} | \overline{u} \times \overline{v}| = \begin{vmatrix} \overline{e_1} & \overline{e_2} & \overline{e_3} \\ 0 & -1 & -2 \\ 1 & -2 & -2 \end{vmatrix}$

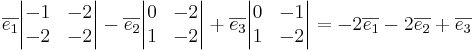
$\overline{e_1} \begin{vmatrix} -1 & -2 \\ -2 & -2 \end{vmatrix} - \overline{e_2} \begin{vmatrix} 0 & -2 \\ 1 & -2 \end{vmatrix} + \overline{e_3} \begin{vmatrix} 0 & -1 \\ 1 & -2 \end{vmatrix} = -2 \overline{e_1} - 2 \overline{e_2} + \overline{e_3}$

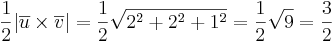$\frac{1}{2} | \overline{u} \times \overline{v}| = \frac{1}{2} \sqrt{2^2 + 2^2 + 1^2} = \frac{1}{2} \sqrt{9} = \frac{3}{2}$ a.e

[edit] b) planets ekvation på affin form

Planets normal (-2,-2,1) eller (2,2,-1).

Planets ekvation 2x + 2y -z +d = 0

vi sätter in en av punkterna:

2x + 2y -z + d = 0

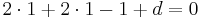
$2 \cdot 1 + 2 \cdot 1 - 1 + d = 0$

d = -3

2x + 2y + z -3 = 0

[edit] Uppgift 4: spegelbilder

Punkterna (1,1,1) och (3,2,2) är varandras spegelbilder i ett visst plan. Bestäm ekvationen för detta plan.

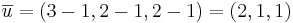
$\overline{u} = (3-1,2-1,2-1) = (2,1,1)$

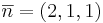
$\overline{n} = (2,1,1)$

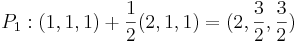
$P_1 : (1,1,1) + \frac{1}{2}(2,1,1) = (2,\frac{3}{2}, \frac{3}{2})$

planets ekvation: 2x + y + z + d = 0

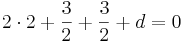
$2 \cdot 2 + \frac{3}{2} + \frac{3}{2} + d = 0$

d = -7

[edit] Svar:

2x + y + z -7 = 0

[edit] Uppgift 5: HON-system

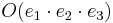$O(e_1 \cdot e_2 \cdot e_3)$ är ett HON-system. I detta har punkten P koordinaterna (2,5,8). Ett nytt HON-system 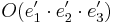$O(e'_1 \cdot e'_2 \cdot e'_3)$ införes så att $e' 1$ blir parallell med planet $3 x + 2 y - z + 1 = 0$ och så att $e' 2$ blir parallell med vektorn (1,1,1). Ange koordinaterna för punkten P i det nya systemet. Flera fall är möjliga. Välj ett!

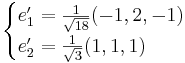
$\begin{cases} e'_1 = \frac{1}{\sqrt{18}} (-1,2,-1)\\ e'_2 = \frac{1}{\sqrt{3}} (1,1,1) \end{cases}$

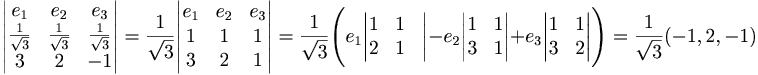
$\begin{vmatrix} e_1 & e_2 & e_3 \\ \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{3}} \\ 3 & 2 & -1 \end{vmatrix} = \frac{1}{\sqrt{3}} \begin{vmatrix} e_1 & e_2 & e_3 \\ 1 & 1 & 1 \\ 3 & 2 & 1 \end{vmatrix} = \frac{1}{\sqrt{3}} \Biggl( e_1 \begin{vmatrix} 1 & 1 & \\ 2 & 1 \end{vmatrix} - e_2 \begin{vmatrix} 1 & 1 \\ 3 & 1 \end{vmatrix} + e_3 \begin{vmatrix} 1 & 1 \\ 3 & 2 \end{vmatrix} \Biggr) = \frac{1}{\sqrt{3}} (-1,2,-1)$

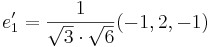
$e'_1 = \frac{1}{\sqrt{3} \cdot \sqrt{6}} (-1,2,-1)$

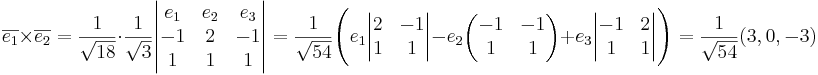
$\overline{e_1} \times \overline{e_2} = \frac{1}{\sqrt{18}} \cdot \frac{1}{\sqrt{3}} \begin{vmatrix} e_1 & e_2 & e_3 \\ -1 & 2 & -1 \\ 1 & 1 & 1 \end{vmatrix} = \frac{1}{\sqrt{54}} \Biggl( e_1 \begin{vmatrix} 2 & -1 \\ 1 & 1 \end{vmatrix} - e_2 \begin{pmatrix} -1 & -1 \\ 1 & 1 \end{pmatrix} + e_3 \begin{vmatrix} -1 & 2 \\ 1 & 1 \end{vmatrix} \Biggr) = \frac{1}{\sqrt{54}} (3,0,-3)$

note Vi struntar i bråktalet, och förkortar.

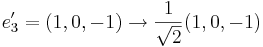
$e'_3 = (1,0,-1) \to \frac{1}{\sqrt{2}} (1,0,-1)$

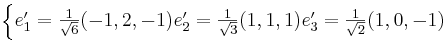
$\begin{cases} e'_1 = \frac{1}{\sqrt{6}} (-1,2,-1) e'_2 = \frac{1}{\sqrt{3}} (1,1,1) e'_3 = \frac{1}{\sqrt{2}} (1,0,-1) \end{cases}$

(Ops... Ovan blev fel...)

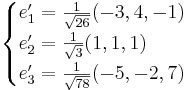
$\begin{cases} e'_1 = \frac{1}{\sqrt{26}} (-3,4,-1) \\ e'_2 = \frac{1}{\sqrt{3}} (1,1,1) \\ e'_3 = \frac{1}{\sqrt{78}} (-5,-2,7) \end{cases}$

$X = S X'$

$X' = S' X$

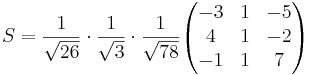
$S = \frac{1}{\sqrt{26}} \cdot \frac{1}{\sqrt{3}} \cdot \frac{1}{\sqrt{78}} \begin{pmatrix} -3 & 1 & -5 \\ 4 & 1 & -2 \\ -1 &1 & 7 \end{pmatrix}$

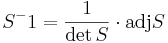
$S^-1 = \frac{1}{\det S} \cdot \mbox{adj} S$

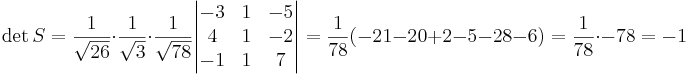
$\det S = \frac{1}{\sqrt{26}} \cdot \frac{1}{\sqrt{3}} \cdot \frac{1}{\sqrt{78}} \begin{vmatrix} -3 & 1 & -5 \\ 4 & 1 & -2 \\ -1 & 1 & 7 \end{vmatrix} = \frac{1}{78} (-21-20+2-5-28-6) = \frac{1}{78} \cdot -78 = -1$

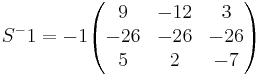
$S^-1 = -1 \begin{pmatrix} 9 & -12 & 3 \\ -26 & -26 & -26 \\ 5 & 2 & -7 \end{pmatrix}$

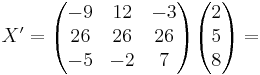
$X' = \begin{pmatrix} -9 & 12 & -3 \\ 26 & 26 & 26 \\ -5 & -2 & 7 \end{pmatrix} \begin{pmatrix} 2 \\ 5 \\ 8 \end{pmatrix} =$

[edit] Uppgift 6: 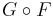$G \circ F$

F och G är två linjära avbildningar enl. följande:

F roterar rummets vektorer vinkeln 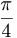$\frac{\pi}{4}$ moturs kring x-axlen, om man tittar i negativa x-axlen riktning.
G roterar rummets vektorer vinkel 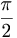$\frac{\pi}{2}$ moturs kring y-axlen, om man tittar i negativa y-axlens riktning.

Bestäm matrisen för den sammansatta avbildningen 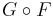$G \circ F$

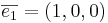$\overline{e_1} = (1,0,0)$ avbildas på (1,0,0)

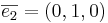$\overline{e_2} = (0,1,0)$ avbildas på $(0,\frac{1}{\sqrt{2}},- \frac{1}{\sqrt{2}})$

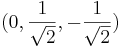
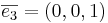$\overline{e_3} = (0,0,1)$ avbildas på $(0,\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})$

$\overline{e_1} = (1,0,0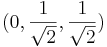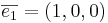)$ avbildas på (0,0,1)

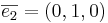$\overline{e_2} = (0,1,0)$ avbildas på (0,1,0)

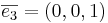$\overline{e_3} = (0,0,1)$ avbildas på (-1,0,0)

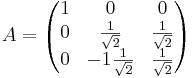
$A = \begin{pmatrix} 1 & 0 & 0 \\ 0 & \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ 0 & -1 \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{pmatrix}$

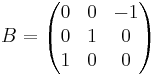
$B = \begin{pmatrix} 0 & 0 & -1 \\ 0 & 1 & 0 \\ 1 & 0 & 0 \end{pmatrix}$

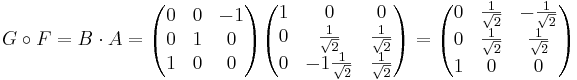
$G \circ F = B \cdot A = \begin{pmatrix} 0 & 0 & -1 \\ 0 & 1 & 0 \\ 1 & 0 & 0 \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 \\ 0 & \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ 0 & -1 \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{pmatrix} = \begin{pmatrix} 0 & \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\ 0 & \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ 1 & 0 & 0 \end{pmatrix}$

[edit] Övnings tenta 2002-06-07

[edit] Uppgift 1: Vilka värden på a?

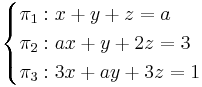
$\begin{cases} \pi_1 : x + y + z = a \\ \pi_2 : ax + y + 2z = 3 \\ \pi_3 : 3x + ay + 3z = 1 \end{cases}$

För vilka värden på a har de tre planen en och endast en gemensam punkt?

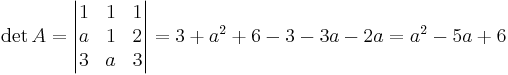
$\det A = \begin{vmatrix} 1 & 1 & 1 \\ a & 1 & 2 \\ 3 & a & 3 \end{vmatrix} = 3 + a^2 + 6 - 3 - 3a - 2a = a^2 - 5a + 6$

$d e t A = 0$

$a 2 - 5 a + 6 = 0$

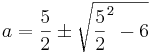
$a = \frac{5}{2} \pm \sqrt{\frac{5}{2}^2 - 6}$

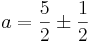
$a = \frac{5}{2} \pm \frac{1}{2}$

$a 1 = 2$

$a 2 = 3$

[edit] Svar:

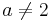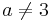
Enligt huvudsatsen så har ekvationsystemet ett entydig lösning när $a \neq 2$ och $a \neq 3$

[edit] Uppgift 5

Kolla att 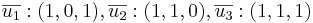$\overline{u_1} : (1,0,1), \overline{u_2} : (1,1,0), \overline{u_3} : (1,1,1)$ är oberoende.

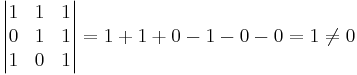
$\begin{vmatrix} 1 & 1 & 1\\ 0 & 1 & 1\\ 1 & 0 & 1 \end{vmatrix} = 1 + 1 + 0 - 1 - 0 - 0 = 1 \neq 0$

Om determinanten är 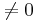$\neq 0$ så är vektorena linjärt oberoende.

[edit] b) bestäm koordinaterna

för 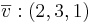$\overline{v} : (2,3,1)$

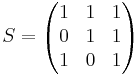
$S = \begin{pmatrix} 1 & 1 & 1 \\ 0 & 1 & 1 \\ 1 & 0 & 1 \end{pmatrix}$

$X' = S - 1 X$

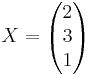
$X = \begin{pmatrix} 2 \\ 3 \\ 1 \end{pmatrix}$

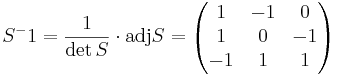
$S^-1 = \frac{1}{\det S} \cdot \mbox{adj} S = \begin{pmatrix} 1 & -1 & 0 \\ 1 & 0 & -1 \\ -1 & 1 & 1 \end{pmatrix}$

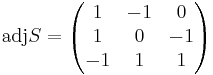
$\mbox{adj} S = \begin{pmatrix} 1 & -1 & 0 \\ 1 & 0 & -1 \\ -1 & 1 & 1 \end{pmatrix}$

(om man vill kan man kontrolera att 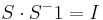$S \cdot S^-1 = I$

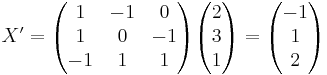
$X' = \begin{pmatrix} 1 & -1 & 0 \\ 1 & 0 & -1 \\ -1 & 1 & 1 \end{pmatrix} \begin{pmatrix} 2 \\ 3 \\ 1 \end{pmatrix} = \begin{pmatrix} -1 \\ 1 \\ 2 \end{pmatrix}$

[edit] Uppgift 6

Speglar rummets vektorer i planet 2x + 3y + z = 0

note Undersök vad som händer med basvektorena

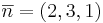
$\overline{n} = (2,3,1)$

(1,0,0) + t(2,3,1) = (1 + 2t, 3t,t)

2(1+2t) + 3(2t) + 1(t) = 0

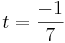
$t = \frac{-1}{7}$

Spegelpunkten Q är två t.

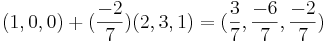
$(1,0,0) + (\frac{-2}{7})(2,3,1) = (\frac{3}{7}, \frac{-6}{7}, \frac{-2}{7})$

calcylations here

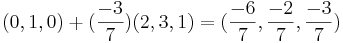
$(0,1,0) + (\frac{-3}{7})(2,3,1) = (\frac{-6}{7}, \frac{-2}{7}, \frac{-3}{7})$

calcylations here

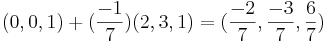
$(0,0,1) + (\frac{-1}{7})(2,3,1) = (\frac{-2}{7}, \frac{-3}{7}, \frac{6}{7})$

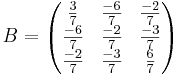
$B = \begin{pmatrix} \frac{3}{7} & \frac{-6}{7} & \frac{-2}{7} \\ \frac{-6}{7} & \frac{-2}{7} & \frac{-3}{7} \\ \frac{-2}{7} & \frac{-3}{7} & \frac{6}{7} \end{pmatrix}$

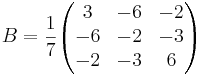
$B = \frac{1}{7} \begin{pmatrix} 3 & -6 & -2 \\ -6 & -2 & -3 \\ -2 & -3 & 6 \end{pmatrix}$

Y = A X

Vill vill ha ut a så vi räkna ut X'.

$X = \begin{pmatrix} 1 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \end{pmatrix}$

$Y = \begin{pmatrix} 1 & 1 & 0 \\ 1 & 0 & 1 \\ 1 & 0 & 0 \end{pmatrix}$

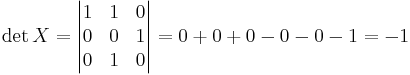
$\det X = \begin{vmatrix} 1 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \end{vmatrix} = 0 + 0 + 0 - 0 - 0 - 1 = -1$

$\mbox{adj} X = \begin{pmatrix} -1 & 0 & 1 \\ 0 & 0 & -1 \\ 0 & -1 & 0 \end{pmatrix}$

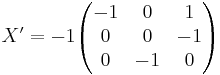
$X' = -1 \begin{pmatrix} -1 & 0 & 1 \\ 0 & 0 & -1 \\ 0 & -1 & 0 \end{pmatrix}$

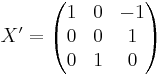
$X' = \begin{pmatrix} 1 & 0 & -1 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \end{pmatrix}$

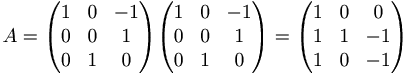
$A = \begin{pmatrix} 1 & 0 & -1 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \end{pmatrix} \begin{pmatrix} 1 & 0 & -1 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0 \\ 1 & 1 & -1 \\ 1 & 0 & -1 \end{pmatrix}$

[edit] Övriga övnings-tentor

note: Tenta 2002-06-07 saknas online

MA1106/Exams

From FUKTwiki

Contents

[edit] Övnings tenta 2006-01-04

[edit] Uppgift 1. För vilka värden på a

[edit] a = 2 ger

[edit] a = -1 ger

[edit] Svar:

[edit] Uppgift 2 a). Lös matrisekvationen

[edit] Svar:

[edit] Uppgift 2 a). För vilka r är matrisen A inverterbar

[edit] Svar:

[edit] Uppgift 3. Beräkna kortaste avståndet

[edit] Svar:

[edit] Uppgift 4 a). Visa att vektorena är linjärt oberoende

[edit] Svar:

[edit] Uppgift 4 b). Bestäm koordinaterna med avseende på basen

[edit] Svar:

[edit] Uppgift 5. Beräkna avståndet mellan linje och punkt

[edit] Svar:

[edit] Uppgift 6. Ange avbildningsmatrisen

[edit] Svar:

[edit] Övningstenta 2007-06-04

[edit] Uppgift 1. Bestäm lösningen till ekvationssystemet

[edit] Svar:

[edit] Uppgift 2 a): Bestäm arean av triangeln

[edit] Svar:

[edit] Uppgift 2 b): Beräkna volymen

[edit] Lös matrisekvationen

[edit] Uppgift 4 a): Linjärt oberoende?

[edit] Svar:

[edit] Uppgift 4 b): Bestäm koordinaterna för vektorn

[edit] Svar:

[edit] Uppgift 5: Koordinaterna för linjen

[edit] Svar:

[edit] Uppgift 6: Spegling och vridning

[edit] A) bestäm matrisen till F

[edit] b)

[edit] C)

[edit] Övnings tenta 2002-03-12

[edit] Uppgift 1 Lös ekvationsystemet

[edit] Uppgift 2 bestäm matrisen X

[edit] Uppgift 3: En triangel

[edit] a) Bestäm arean

[edit] b) planets ekvation på affin form

[edit] Uppgift 4: spegelbilder

[edit] Svar:

[edit] Uppgift 5: HON-system

[edit] Uppgift 6:

[edit] Övnings tenta 2002-06-07

[edit] Uppgift 1: Vilka värden på a?

[edit] Svar:

[edit] Uppgift 5

[edit] b) bestäm koordinaterna

[edit] Uppgift 6

[edit] Övriga övnings-tentor

Views

Personal tools

Navigation

FUKT

Search

Navigation

FUKT

Search

Toolbox

[edit] Uppgift 6: $G \circ F$