ET1206/Lectures
From FUKTwiki
[edit] 2007-11-05
[edit] 3.1 Kryptering
- ke = hemlig nyckel
- m = meddelande
- c = krypterad text
- m → (ke,m) → c
- c = E (ke,m) ⇒ c send
- E = krypterings funktioner (algoritmer)
- Rx ← In = c
- m = D (ke, c)
- D = dekrypterings funktion
- resultat m.
Exempel: "sjörövarspråket" m = Ronneby ke = o krypteringsfunktionen = E = ett ke skall införas efter varje konsonant och konsonanten före varje ke skall repeteras efter varje ke.
c = rorononnoneboby
skicka c
dekrypteringsfunktin = D = för varje hittat ke, kolla om det är en konsonant före och efter varje ke. om de är lika, tag bort första + ke
resultat = m = D("o", "roronnoneboby") = Ronneby
[edit] Kerckhoffs' principle
The security of the encryption scheme depends on the secrecy of ke, not on how public the information of how E or D works.
Fortfarande möjligt
- att byta hela meddelandet
- ta bort meddelandet
- ändra ordningen
[edit] 3.2 Autentisering, verifiering
- ka = Authentication key
- Tx ← m = medelande
- a = MAC = message authentication code
- a = MAC = h(ka,m)
Send: a,m
Rx ← In a,m
beräkna a
a = h(ka,m)
Resultat: Mottagit a och beräknat a.
[edit] 3.3 Public key encryption (publika nycklar)
Problem: Hur ska vi dela med oss nycklarna på ett säkert sätt?
| 2-persons | byt nycklar, snigelpost |
| 3 | 3 byten |
| 4 | 6 byten |
| 1000 | 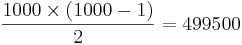 byten byten |
Lösning: använd publika nycklar
- Bob generates 2 nycklar
- Hemlig nyckel ksbob
- Publik nyckel kpbob
kpbob publiceras av Bob
Alice ska skicka till meddelande till Bob.
- Hämta publika nyckeln kpbob
- Kryptera meddelandet C = E(kpbob,m)
Bob får meddelandet
- Använder sin hemliga nyckel ksbob
- Dekryptera meddelandet m = D(ksbob,c)
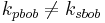
- kpbob kan inte i praktiken räknas fram från kpbob
- Enklare för större grupper att kommunicera säkert
[edit] 3.4 Digitala signaturer
Alice genererar två nycklar. kpalice ksalice
Alice genererar sedan en signatur.
- Genom att använda hemliga nyckeln ksalice
S = σ(ksalice,m)
Alice skickar S, m (och sin publika nyckel kpalice))
Bob tar emot S, m
- Använder publika nyckeln kpalice
- Verifierar signaturen S = v(kpalice,m)
- Jämför beräknad signatur med mottagen
[edit] 2007-11-06
kryptering, hemlig nyckel
ke C = E(ke,m)
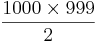
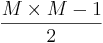
[edit] Publika nycklar
kpbob,ksbob
C = E(kpbob,m)
m = D(ksbob,c)
[edit] 3.5 PKI, Public Key Infrastructure
Problem: hur vet vi att kpbob verkligen tillhör Bob?
Lösning: CA = Certified[sic] Authority
CA använder en digital signatur för att säkerställa att verkligen kpbob tillhör Bob.
Certifikat
[edit] 3.6 Attacker
[edit] 1 Ciphertext only
Attackera den krypterade texten
[edit] 2 Known plain text
Attackera och försök komma åt nyckeln
Exempel: Du kommer åt både c, m
någon skickar ett mail där du är en av mottagarna.
[edit] 3 Chosen plain text
Attackera och försök få nyckeln.
Exempel: Jag skickar meddelande till Alice som forwardar krypterat.
[edit] 4 Chosen Ciphertext
?
[edit] Collision attacks
- Birthday attack
23 personer P(två har samma födelsedag) > 0,5
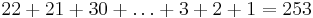
365 dagar på ett år ⇒ 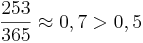
Attacker som grundar sig på att kopior på nycklar och meddelande uppkommer fortare än man tror.
[edit] 4 Blockkryptering
Block cipher: krypteringsfunktion för en fix blockstorlek, t.ex. 128 bitar.
- Blockstorlek av originaltext och krypterad text lika stora.
- Storleken av nyckeln är oftast 128 eller 256 bitar
- C = E(K,p)
- P = D(K,c)
- E(K,p) = Ek(p) krypteringsfunktion publik
If P > 128, use block cipher mode (kapitel 5).
Ek(p)
| P | c |
|---|---|
| 00 | 11 |
| 01 | 00 |
| 10 | 01 |
| 11 | 10 |
Dk(c)
| c | p |
|---|---|
| 00 | 01 |
| 01 | 10 |
| 10 | 11 |
| 11 | 00 |
- En tabell för varje nyckel
Block length = 2(block size) = 22 = 4rows
Verkligheten: 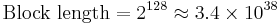
Attacker: för att få bra resultat använd chosen plain text
Ek(p)
| P | c1 | c2 |
|---|---|---|
| 00 | 11 | 00 |
| 01 | 00 | 11 |
| 10 | 01 | 01 |
| 11 | 10 | 10 |
[edit] 4.3 The Ideal block cipher
För varje ny nyckel: slumpmässig look-up-tabell
[edit] 4.5 Real block ciphers
- Hitta ej på er egen algoritm
Egenskaper:
- Använd XOR för att addera på nyckeln
- Använd S-box för att lägga till non-linearity
- Vänd och vrid på bitarna för att skapa oordning (mål: En liten ändring i klartexten ska göra stor ändring i kryptotexten)
- Kör algoritmen flera "rounds"
[edit] DES
Data Encryption Standard (1970-talet)
(Gammal, obsolete)
Nyckelstorlek = 56 bitar
Blockstorlek = 64 bitar
64 bitar, 32L och 32H.
Runda 0:
- L0 = 32L
- R0 = 32R
Runda 1:
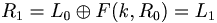
- L1 = R0
Funktion F
- Expandera R från 32 → 48 bitar
- XOR med nyckeln ki som är 48 bitar och olika för varje rounds.
- The S-box: 8 st
- Blanda de 32 bitarna
- Klart för en runda till
Denna struktur kallas Feistel construction
Nycklar så väljs kj (48 bitar) ut på ett speciellt sätt från originalnyckeln på 56 bitar.
[edit] 2007-11-07
[edit] 4
Blockstorlek 128 in ⇒ 128 bitar ut
| 00 | 01 |
| 01 | 11 |
| 10 | 00 |
| 11 | 10 |
2128
DES (Data encryption Standard)
| key 56 | Blocks = 64 |
3DES
key 128
Nackdelar:
- Fortfarande blockstorlek 64
- Långsam
- Vad händer om k = 0 (alla bitar 0)?
Fördel:
- Använder samma hårdvara för kryptering som dekryptering
[edit] AES
NIST (National Institute of Standards and Technology)
AES (Advanced Encryption Standard)
krav:
- Blockstorlek 128 bitar
- Nyckelstorlek: 128, 192 eller 256
15 förslag ⇒ 5 finalister
2001 ⇒ Rijndael
Rijndael var det möjligt att variera blockstorleken [128], 192, 256
{{subst:AES}}
[edit] Lineraritet
![\begin{align}
A & \to & [F] & \to & AA \\
B & \to & [F] & \to & BB \\
A+B & \to & [F] & \to & AA+BB
\end{align}](upload/images/math/c/0/7/c0736f7e7d4c1593aa8af781939eb41c.png)
![\begin{align}
A & \to & [F] & \to & A^2 & \\
B & \to & [F] & \to & BB & \to \mbox{Detta är EJ LINJÄRT!} \\
A+B & \to & [F] & \to & AA+BB &
\end{align}](upload/images/math/5/9/2/59212720ad26a8577a6eddfcb2f21ce4.png)
[edit] Subbytes
8 bitar → Sbox → 8 bitar
Alla S-boxar är identiska
[edit] Shiftrows
Byter "bytes" i samma rad plats genom att skifta 1-3 positioner beroende på rad
[edit] Mix Columns
Varje kolumn i blocket multipliceras med en förutbestämd matris så att varje "byte" får ett nytt värde.
[edit] Add Round Key
Xor med data och nyckel (permutation av originalnyckeln; olika varje runda).
| AES | rounds |
|---|---|
| 128 | 9 |
| 192 | 12 |
| 256 | 14 |
[edit] Fördel mot DES
- Större nyckel
- Större blockstorlek
- AES är mindre komplex än 3DES
[edit] Serpent
Alternativ till AES
Säkrare än AES ⇒ mer komplex
[edit] Twofish
Mellanting mellan AES och Serpent
Snabbt att kryptera, långsamt att byta nyckel och i början med ny nyckel
[edit] Attacker
[edit] XSL - equation solving attacks
Exempel: AES 128 blir 8000 ekvationer med 16000 variabler
[edit] Which block cipher should I use?
[edit] Vilken nyckelstorlek ska jag använda?
| Minst betydelse | |
| ⋮ | |
| 128 bitar | Bra nog, men se upp med collision attacks |
| ⋮ | |
| 256 bitar | AES 256 är mycket långsammare än AES 128 |
| ⋮ | |
| Mest betydelse |
Rule: For a security level of n bits, every cryptographic value should be at least 2n bits long.
[edit] 2007-11-12
[edit] 5 Block Cipher Modes
Det är problem om två krypterade block Ci är lika.
Ci = E(K,Pi)
Ck = E(K,Pk)
Ci = Ck ⇒ Pi = Pk, vilket blir mycket lättare att knäcka.
[edit] Kollisionsrisk för två Ci block
[128 bitar] ↔ [128 bitar]
Sannolikheten att dessa två block är lika är 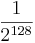 .
.
Om vi skickar M block över kanalen, vad är sannolikheten att två av dessa är lika? 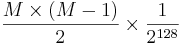
meddelandet är längre än 1 block (oftast 128 bitar – 16 ”byte”).
[edit] 5.1 Padding
Bara addera nollor på slutet är ingen bra idé. Det är svårt att veta hur många som ska tas bort vid dekrypteringen.
Vi behöver något padding-schema.
P = plaintext
l(P) = längden av meddelandet
b = blockstorleken i ”bytes”
[edit] Schema
"Meddelande" + bin(128) + bin(0)+ upp till b ”bytes”.
Exempel:
"AB" ⇒ (om b = 4) ⇒ "AB", bin(128), 0
Detta fungerar inte där ”byten” 128 kan förekomma.
[edit] Schema 2
Beräkna hur många padding-”bytes” som behövs för att få ett fullt block. 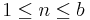
Lägg till meddelandet med n ”bytes” av värde bin(n).
Exempel: ”AB” → ”AB” + bin(2) + bin(2)
[edit] 5.2 ECB – Electronic Code Book
(Ska ej användas.)
Ci = E(K,Pi) för 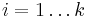
Om två Pi är lika ⇒ två Pi lika.
Inte bra för en attack.
[edit] 5.3 CBC – Cipher Block Chaining
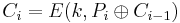
Löser problemet med att om två Ci = Ck ⇒ Pi = Pk
Problem? Hur hittar vi C0 = Initialization Vector, IV?
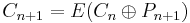
[edit] 1 Fix IV eller C0
Om flera meddelanden har samma start:
P1 kommer vara samma ⇒ C1 kommer att vara samma.
Inte bra ur en attacksynpunkt.
[edit] 2 Counter IV
IV = 0 för första meddelandet, IV = 1 för andra, o.s.v.
Om skillnaderna är små i meddelandet är det risk att XOR inte ger så stora skillnader.
[edit] 3 Random IV
Slumpmässig C0, mottagaren måste också veta samma C0.
C0 = random block value
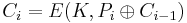
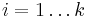
Dekryptering:
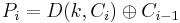
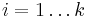

Nackdel:
- Slumpgenerator behövs
- Vår krypterade text förlängs med ett block
[edit] 2007-11-13
[edit] CBC – Cipher Block Chaining (forts.)
[edit] Nonce generated IV
Number used only once
Så att C0 får bara användas en gång med varje nyckel K.
(Varje meddelande har oftast redan ett löpnummer.)
- Konstruera ett nonce (128 bitar)
- Kryptera E(k,nonce) = C0
- Kryptera hela meddelandet genom att använda CBC
- Dekryptera meddelandet och kontrollera nonce
Exempel:
p = "HEJ"
blockstorlek två ”bytes”
CBC
C0 = random = 0000111100001111
k = 0101010101010101
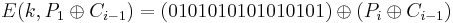
P1 = (ASCII(H) = 72, ASCII(E) = 69)
P2 = (ASCII(J) = 74, padding)
| ASCII | Dec | Bin |
|---|---|---|
| H | 72 | 01001000 |
| E | 69 | 01000101 |
| J | 74 | 01001010 |
Padding = 128
P1 = 0100100001000101
P2 = 0100101010000000
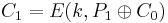
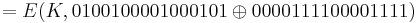 = E(K,0100011101001010)
= E(K,0100011101001010) 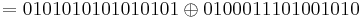 = 0001001000011111
= 0001001000011111
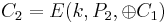
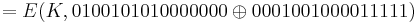 = E(K,0101100010011111)
= E(K,0101100010011111) 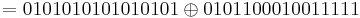 = 0000110111001010
= 0000110111001010
Dekryptering:
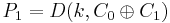
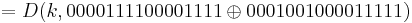 = D(k,0001110100010000)
= D(k,0001110100010000) 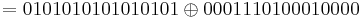 = 0100100001000101
= 0100100001000101
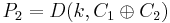
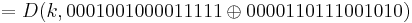 = D(k,0001111111010101)
= D(k,0001111111010101) 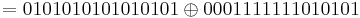 = 0100101010000000
= 0100101010000000
[edit] Stream Ciphers
Vi använder inte blockkrypteringen på meddelandet P1, utan vi använder blockkrypteringen för att skapa en pseudorandom sekvens av bitar som vi sedan kör XOR på meddelandet
[edit] OFB – Output Feedback Mode
K0 = IV
IV skapas enligt ovan
ki = E(K,ki − 1) för 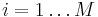
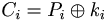
IV genereras och skickas.
Fördelar: kryptering samma som dekryptering
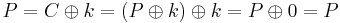
Behöver ingen padding. ”Bra för små meddelanden”, står det i boken.
Nackdel: Om man använder samma IV (K0) så kommer två meddelanden att kodas med samma ström.
Två meddelanden p och p' kodas med samma ström ki ⇒ två krypton C och C'
Attackeraren gör följande:

[edit] CTR – Counter Mode
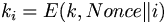 för
för 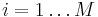
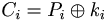
Där Nonce är unik för varje meddelande
i är blocknummer i meddelandet
Typiskt:
| 48 bitar | meddelandenummer |
| 16 bitar | nonce |
| 64 bitar | för räknaren i |
[edit] 2007-11-14
[edit] CTR – Counter Mode (forts.)
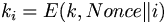
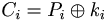
[edit] OFB
K0 = IV
Ki = E(K,ki − 1)
[edit] Exempel
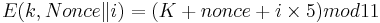
Blockstorlek 8 bitar, K = 3, nonce = 7, i = 0
| i | ki | ki binärt | |
|---|---|---|---|
| i=0 | 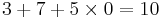 |
10 | 00001010 |
| i=1 | 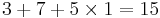 |
4 | 00000100 |
| i=2 | 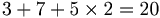 |
9 | 00001001 |
P = "HEJ" = ASCII(H), ASCII(E), ASCII(J) = 0x48, 0x45, 0x4A
P0 = 01001000
P1 = 01000101
P2 = 01001010
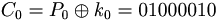
C1 = 01000001
C2 = 01000011
Vi ska använda CBC eller CTR
| CBC | CTR | |
|---|---|---|
| Padding | Ja | nej |
| Hastighet | Snabb | Snabbare, ty parallel processing |
| Implementering | både E och D | bara E |
| Robust | läcker information om första blocket | läcka information om hela meddelandet |
| Nonce | Behövs, ev. random | Behövs |
[edit] 5.8 Läckor
- ECB (Electronic Code Book)
- Om
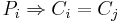
- CBC (Cipher Block Chaining)
- Om
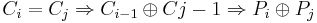
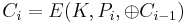
Ci = Cj
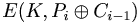
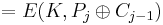
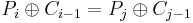 ...
...
- CTR
- Om Pi = Pj blir inte Ci = Cj
Däremot så om 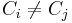 så är
så är 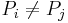 ⇒ väldigt lite information som läcks.
⇒ väldigt lite information som läcks.
[edit] Risk för kollision
M block skickas, varje block har längden n bitar.
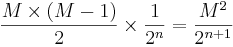
Detta 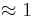 om M = 2n / 2. Om n = 128 så får vi kollision om M = 264
om M = 2n / 2. Om n = 128 så får vi kollision om M = 264
[edit] 6 Hashfunktioner (kryptografiska hash functions)
Används för authentication (verifiering) digitala signaturer
Godtycklig mängd → hash → begränsad mängd, t.ex. 512 bitar
Istället för att signera m direkt så signerar man m' = h(m) där h är hashfunktionen.
[edit] 6.1 Säkerhet med hashfunktioner
- En-vägs funktion, inte möjligt att skapa m från m'
- Kollision:
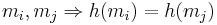
Kollisionsresistenta funktioner = Även om kollisioner finns så inträffar de aldrig.
Ideal hashfunktion = slumpmässig mappning från alla möjliga insignaler till en begränsad mängd utsignaler.
hashfunktioner ⇒ ingen nyckel behövs
[edit] Praktiska hashfunktioner
Iterativa hashfunktioner som MD5 och SHA-familjen.
- Dela upp meddelandet i block, k stycken (plus ev. padding).
- Varje block processas för sig
Start: H0
Hi = h'(Hi − 1,mi) där m = meddelandeblock i och Hk är slutgiltiga resultatet.
[edit] Fördelar med iterativa hashfunktioner
- Enklare att implementera
- Kan börja köra innan hela m mottagits
[edit] MD5
- 128 bitars output
- Meddelandet delas upp i block om 512 bitar
- Sista blocket innehåller meddelandets längd och padding
h' rekursiv den körs 4 rundor där varje runda innehåller additioner, booleansk algebra och blandning (permutering)
Nackdel: h' har kollisioner ⇒ H har kollisioner.
[edit] SHA-1
- 160 bitars output
- 2-3 gånger långsammare än MD5
- Blockstorleken är 128 bitar
SHA-256, SHA-384, SHA-512: Storleken på output för dessa varianter är 256, 384 respektive 512.
[edit] 2007-11-19
[edit] 6 Hashfunktioner
"Hash" = hacka sönder, röra om
m:h(m) = H
[edit] Iterativa hashfunktioner
Kan pipe-line:as.
m delas upp i block om n bitar, t.ex. 512.
H0
Hi = h'(Hi − 1,mi)
H = Hk där
[edit] 6.3 Svagheter hos hashfunktioner
[edit] Length extensions
Första meddelandet m innehåller k block (och ev. delblock).
Andra meddelandet m' innehåller k + 1 block och de första k blocken är lika som i meddelande m.
| m | |||
|---|---|---|---|
| A | B | C | |
| m' | |||
| A | B | C | p |
Första meddelandet: H = h(m)
Andra meddelandet: H för de första k blocken = h(m), H för alla block 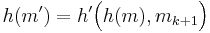
MAC
[edit] 6.3.2 Partial message collision
Meddelande m
Verifiering av meddelandet (MAC) 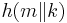
k = nyckel
Attacker
Brute force to find k
Om en iterativ hashfunktion används för att räkna ut H då kan vi göra en bättre attack.
Leta efter två meddelande m och m' som ger en "kollision", d.v.s. som har samma H.
2n / 2 försök behövs, vilket är mycket enklare är att finna k.
[edit] Fix av svagheterna
kör hashfunktionen två gånger
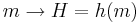
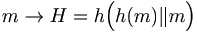
Löser svagheterna
- Långsamt
- Behöver buffra hela meddelandet
En bättre fix
Bibehålla hastigheten (tidskomplexiteten)
H = h(m)
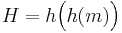 vi använder bara n / 2 bitar för att bibehålla hastigheten.
vi använder bara n / 2 bitar för att bibehålla hastigheten.
kallas hd t.ex. SHAd-256.
[edit] 7 Message Authentication Codes (MAC)
Kryptering hindrar Eva från att läsa meddelande, men inte att manipulera dem.
Authenticering hindrar att Eva kan manipulera med meddelanden, men inte att läsa dem.
Alice
a = MAC(k,m)
a,m skickas
Bob
a' = MAC(k,m) jämför a och a'.
[edit] 7.4 CBC-MAC
Kombinera Block cipher mode och MAC.
- Kryptera meddelandet m genom att använda CBC
- Kasta bort alla krypterade block Ci utom det sista Ck = a
Meddelande 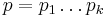
H0 = IV
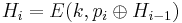
a = MAC = Hk
IV som vanligt IV = 0 IV = random
OBS! Använd inte samma nyckel vid kryptering och verifiering.
Säkerhet på 128 bitar använder CBC-MAC om 256 bitar.
[edit] 7.5 HMAC (Hash MAC)
Ej ideal hashfunktion ⇒ Hashsäkerhet = n / 2 bitar
”Bra” MAC: 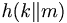 om h är bra.
om h är bra.
[edit] 7.6 UMAC
Samma som HMAC fast snabbare.
T.ex. UMAC-STD-30, UMAC-MMX-30
Horton principle: Man ska ska authenticera vad som menas, inte vad som sägs.
T.ex. verifiera inte bara på IP-paket-nivå, då vet vi ju inte hur mailprogrammet tolkar data.
[edit] 2007-11-20
[edit] 8 The Secure Channel
- K är bara känd av Alice och Bob.
- Varje gång man sätter upp en ny kanal genereras ett nytt värde från nyckeln K för att Eva inte ska kunna använda meddelande från äldre sektioner.
- Key negotiation protocol
[edit] Trafikanalys
Alice ↔ Bob
- Storlek på m
- Tidpunkt
- Vem skickar meddelande till vem
[edit] 8.2 Ordningen på kryptering och verifiering
[edit] Kryptering först
Kryptering först för sändaren, verifiering först för mottagaren.
- ”Teoretiska resultat visar att kryptering först är bäst.”
- Mer effektivt vid fejkade meddelanden.
[edit] Autentifiering (verifiering) först
- MAC krypteras också. Det viktigaste är att skydda MAC.
- Authenticate what is being meant (klartexten), not what is being said (krypterade texten).
Recommended: Verifiera först, kryptera sedan.
[edit] 8.3 Hur sätter vi upp en säker kanal?
- Meddelandenumreringen – nonce
- Verifiering
- Kryptering
[edit] 8.3.1 Meddelandenumrering
- Källa för att finna IV
- Säkerställa att Bob får meddelandena i rätt ordning
- Unika
- Monotont växande
Använd 32 bitar ⇒ max antal meddelanden 232 − 1, därefter byt nyckel.
m är index; meddelandenummer.
[edit] Authentication (verifieringen)
Använd HMAC – SHA-256
Insignal pm meddelande och xm är extra verifieringsdata (protokoll, typ av meddelande).
MAC code = am
l(.) = längden av en sträng i ”bytes”
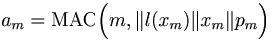
[edit] Krypteringen
AES (Advanced Encryption Standard) in CTR mode with nonce.
Blockstorlek 128 bitar (16 ”bytes”).
Maxstorlek på varje meddelande 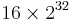 bytes ⇒ blockräknare på 32 bitar med index i.
bytes ⇒ blockräknare på 32 bitar med index i.
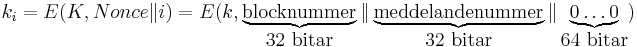
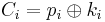
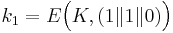
[edit] 2007-11-21
[edit] 10 Generera slumptal
Mättal för slumpmässighet ”entropy”
Exempel: 32 bitars tal ⇒ entropy = 32 bitar
Om 31 bitar + en bit paritet ⇒ entropy = 31 bitar
[edit] 10.1.2 Pseudorandom data (PRNG)
p(x) ↑
│
│
1 ├──┐
│░░│
│░░│
└──┴──→
0 1 x
Slumptal framräknade med en matematisk algoritm från ett startvärde (seed) är slumpmässiga från en statistisk synvinkel, dock inte från en kryptografisk synvinkel.
[edit] 10.3 Fortuna
- Ett riktigt slumptal för att beräkna startvärdet (seed)
- Använd startvärdet för att beräkna en riktig pseudorandom sekvens av valfri längd.
- Ibland byt startvärde och starta generera igen.
[edit] 10.4 Generatorn ska vara en CTR mode
ki = E(K,i)
E ska implementeras av t.ex. AES-algoritmen.
Blockstorlek 256 bitar och räknaren i ska vara 128 bitar.
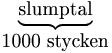 |
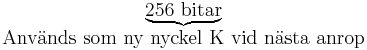 |
Glöm inte bort att ta bort den gamla nyckeln.
Om vi genererar 2128 block med slumpdata så är två block lika ⇒ Begränsa antal block till högst 216 i varje anrop.
[edit] 10.4.1 Initialisering
K = 0 C = counter = 0
[edit] 10.4.2 Reseed
När en viss tid eller viss mängd data överförts.
K = newK
Nytt K kan beräknas med en hash t.ex. SHA-256.
C = C + 1
[edit] 10.4.3 Generate Blocks
Genom att använda CTR
r = E(K,c) (c = counter)
Generera två extra block av r som används som ny nyckel.
[edit] 10.5 Accumulator
Används som insignal till ”reseed”.
Man lägger ihop data från olika källor.
[edit] 10.5.2 Pool
Mängd av händelser som används som input till Ackumulatorn, t.ex. zenerdiodbrus, muspekare.
Viktigt
- Lita aldrig på algoritmer i operativsystemet som genererar slumptal.
- Använd så många händelser som möjligt för att bygga upp ”original”-slumptalet.
[edit] 2007-11-26
[edit] 11 Primtal
Används för generering av publika nycklar
Delbarhet a | b ⇒ a är en delare till b ⇒ Vi kan dela b med a utan att få en rest.
Exempel: 7 | 35 Ja, det är en delare
Primtal: a | 11
Primtal: Om det bara finns två delare: primtalet själv och 1.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
Stryk 1
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
Stryk varannat tal efter två:
| 2 | 3 | 5 | 7 | 9 | |||||
| 11 | 13 | 15 | 17 | 19 | |||||
| 21 | 23 | 25 | 27 | 29 |
Stryk var tredje tal efter tre:
| 2 | 3 | 5 | |||||||
| 11 | 13 | 17 | 19 | ||||||
| 23 | 25 | 29 |
Stryk var femte tal efter fem:
| 2 | 3 | 5 | |||||||
| 11 | 13 | 17 | 19 | ||||||
| 23 | 29 |
Vi kan sluta vid 5, eftersom det är det största tal vars kvadrat är mindre än det högsta tal som ska undersökas.
Lemma 1: a | b och 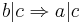
Bevis: Om a | b så måste det finnas ett heltal s så att 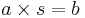 .
.
Om b | c så måste det finnas ett heltal t så att 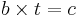 .
.
⇒ 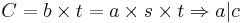
Lemma 2: Låt n vara ett positivt heltal > 1 Låt d vara den minsta delaren till n > 1; då är d ett primtal.
Teorem: Det finns oändligt många primtal.
OBS! Det finns ingen exakt formel för att räkna ut primtal i ett visst intervall.
Goldbach’s conjecture: Varje jämt heltal > 2 är en summa av två primtal.
[edit] 11.3 Moduloräkning med primtal
Exempel: 25mod 7 = 4
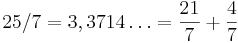
Att finna (amod b) hitta heltalen q och r så att a = qb + r 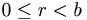 då är (amod b) = r
då är (amod b) = r
[edit] Addition och Subtraktion
(a + b)mod p 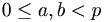
(a + b) är större än p: då blir resultatet a + b − p
Exempel: Om p = 7
5 + 3 − 7 = 1
[edit] Finita fält
Är ett antal heltal modulo ett primtal. Kallas (mod p)-fält eller bara (mod p)
Exempel: Grupp 0,1,2,3,4 och p = 5
Alla resultat kommer att vara i området 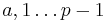 oberoende av operation.
oberoende av operation.
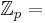 finit fält modulo p
finit fält modulo p
Grupp: Ett antal heltal samt en operation:
Exempel: 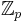 och addition blir en grupp.
och addition blir en grupp.
Exempel: En grupp: { 0, 1, 2, 3, 4, 5, 6, 7 } modulo 8
Detta är inte ett finit fält eftersom 8 inte är ett primtal.
En undergrupp { 0, 2, 4, 6 }
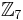 , multiplikativ grupp
, multiplikativ grupp
{ 0, 1, 2, 3, 4, 5, 6 }
A subgroup: { 1, 2, 4 }
Exempel: 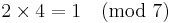
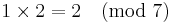
[edit] GCD (Största gemensamma delare )
GDC av (a,b) alltså det största k som uppfyller k | a och k | b
(a,b) = (21,30)
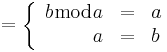
så länge som 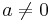
30mod 21 = 9
(a1,b1) = (9,21)
21mod 9 = 3
(a2,b2) = (3,9)
9mod 3 = 0
(a3,b3) = (0,3)
Exempel:
(23,35) = (a0,b0)
[edit] 2007-11-27
[edit] 12.1
[edit] Grupper och undergrupper
{ 0, 1, 2, 3, 4, 5, 6, 7 } (mod 8) är en additiv grupp, men ej ett finit fält eftersom 8 ej är ett primtal.
{ 0, 2, 4, 6 } (mod 8) är också en giltig additiv grupp eftersom man bara kan få någon medlem i gruppen när man adderar medlemmar i gruppen.
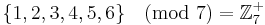
Noll får inte vara med i multiplikativa grupper.
{1,6}
[edit] Diffie och Hellman
1976
10 användare behöver byta 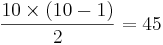 nycklar.
nycklar.
Diffie och Hellman ⇒ Kryptering ≠ Dekryptering
p ska vara ett stortprimtal någonstans i området 2000-4000 bitar.
Finit grupp 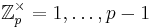 tillsammans med multiplikation modulo p.
tillsammans med multiplikation modulo p.
Skapa en serie: 
g ska vara ett element i gruppen.
Det är en oändlig serie men en finit grupp.
Exempel: 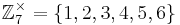
g = 2
Serien: 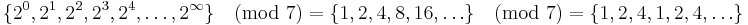
Antag att värdena börjar repeteras vid gi = gj
i < j
Dividera båda sidor med gi ⇒ 1 = gi − j Vi kan finna ett värde q = j − i som ger gqmod p = 1
Minsta möjliga q = ordningen av g ⇒ 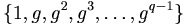
Nästa tal i ordningen är då gq = 1
Exemplet ovan 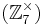
g = 2 genererar serien {1,2,4} ordning q = 3
Det är alltid möjligt att hitta en generator g som kan generera hela gruppen 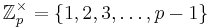
Den generator g som genererar hela gruppen kallas ett primitivt element.
Andra värden på g kommer att generera undergrupper vars storlek är intressant ur en attacksynvinkel.
Välj g som ska vara ett primitivt element (som kan generera hela gruppen).
Välj h som är ett godtyckligt element i gruppen.
⇒ h = gx där x ännu inte är valt.
Element som genereras med hjälp av h: 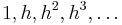
Ordningen av h: det minsta q för vilket hq = 1 ![[ h = g^x ] \Rightarrow g^{xq} = 1](upload/images/math/8/e/b/8eba67a64a13754d1163e00b184a57cc.png)
Om xq = 0(mod p − 1)
Detta händer.
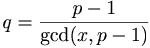
⇒ q är en faktor i p − 1
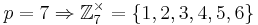
g = primitivt element = 3
Serien 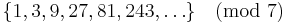
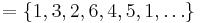
Välj 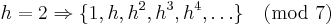
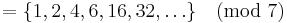
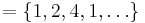 = en subgrupp av ordning 3
= en subgrupp av ordning 3
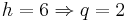
Ordningen av subgrupperna är en faktor av (p − 1)
[edit] 12.2
Exempel
Välj ett primtal: p = 7
Välj ett primitivt element g = 3
p och g är publika.
{1,2,3,4,5,6}
Typisk tentafråga
[edit] Alice
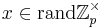 Exempel x = 4
Exempel x = 4
x är hemlig.
Beräkna gx = 34mod 7 = 4
gx är publik
K = (gy)xmod 7 = 24mod 7 = 2
[edit] Bob
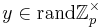 Exempel y = 2
Exempel y = 2
y är hemlig.
Beräkna gy = 32mod 7 = 2
gy är publik
K = (gx)y = 42mod 7 = 2
2 är den gemensamma nyckeln som används vid kommunikationen.
Är det möjligt att beräkna gxy från g, p, gx och gy?
Diffie-Hellman-problemet inte möjligt att lösa om p är ett primtal och om g är ett primitivt element.
Anfallaren känner till p, g och ser gx och gy; känner ej till x och y.
[edit] 2007-12-03
(Cancelled due to illness.)
[edit] 2007-12-04
[edit] Diffie-Hellman
Välj p = 7, välj g = 3
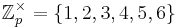
[edit] Alice
Väljer x
Publicerar gx.
k = (gy)x
[edit] Bob
Väljer y
Publicerar gy
k = (gx)y
[edit] 12.3 Man in the middle
[edit] 12.4 Fallgropar
- Fallgrop A
- g = 1 ej bra ty k är alltid = 1
- Lösning: kolla om gx = 1 eller gy = 1
- Fallgrop B
- Generator
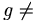 primitivt element, g har en liten subgrupp ⇒ få möjliga nycklar
primitivt element, g har en liten subgrupp ⇒ få möjliga nycklar - Lösning: Kolla så att p = primtal och g = primitivt element eller ger tillräckligt stor subgrupp
OBS. Storleken på subgrupperna är delare till p − 1 så se till att undvika primtal med små delare.
[edit] 12.5 Safe Primes
2q + 1 där q också är ett primtal.
Subgrupper som är möjliga
- Storlek 1: Enkel att testa
- Storlek 2: Nummer 1 och p − 1
- Storlek q Välj denna
- Storlek 2q (fulla gruppen)
[edit] Problem med den fulla gruppen
Exakt hälften av alla tal i en full grupp är ”squares” (mod p)
Exempel: 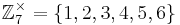
”squares” = {1,4,9,16,25,36,}(mod 7) = {1,4,2,2,4,1}
Non-squares = {3,5,6}
Om en generator g = ”square” ⇒ g är inte ett primitivt element.
p = 2q + 1
Om gx är genererat från en non-square-generator så kan Eve använda sig av Legendre symbol-funktion för att bestämma om x är jämn eller udda.
Lösning: använd g som är ”squares” (mod p) d.v.s. en subgrupp av storlek q
[edit] Algoritm för att använda ett säkert primtal (p,q,g)
- Välj p och q så att både p och q är primtal. p = 2q + 1
- Välj g som är en ”square” så att gx tillhör halva mängden. Hur? Välj α
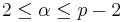 ska uppfylla g = α2(mod p)
ska uppfylla g = α2(mod p) - Kolla så att
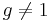 och
och 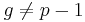
Exempel: q = 5
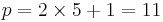
α = 2
g = 22 = 4mod 11 = 4
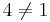 så OK
så OK
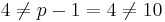 så OK
så OK

gx ger samma möjliga nycklar som (gx)y
gx (ordning q = 5) 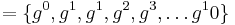
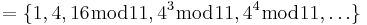 = {1,4,5,9,3}
= {1,4,5,9,3}
När man tar emot ett gx se till att gx kommer från en subgrupp med ordning q
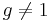 och (gx)qmod p = 1
och (gx)qmod p = 1
Exempel: p = 11 q = 5 g = 4
x = 1 ⇒ gx = 4
(gx)qmod p = (45)mod 11 = 1024mod 11 = 1 ⇒ OK
Om gx = 8
85mod 11 = 32768mod 11 = 10 ⇒ inte OK gx
Säkra primtal har en nackdel att de är beräkningskrävande ⇒ mindre subgrupper.
Hur:
- Hitta ett primtal q minst 256 bitar
- Hitta ett mycket större primtal p = Nq + 1 (om N är primtal är p garanterat primtal)
- Hitta lämpligt g, välj
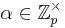 g = αN kolla så att
g = αN kolla så att 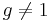 och gq = 1
och gq = 1
[edit] 2007-12-10
[edit] 13 RSA
- Mest kända och använda publika nyckel-krypteringsalgoritmer.
- Både kryptering och digitala signaturer
- Bygger på svårigheten att faktorisera stora primtalsprodukter
[edit] Diffie-Hellman
p och q givna
Lätt att beräkna gxmod p om man vet x, mycket svårt i motsatt riktning.
[edit] RSA
Givet n och e - (publika)
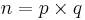 - (inte modulo)
- (inte modulo)
p och q - (stora primtal, minst tusen bitar)
Kryptering: memod n
[edit] 13.2 CRT – The Chinese Remainder Theorem
Diffie-Hellman: Beräkningar modulo ett primtal p
RSA: Beräkningar modulo en primtalsprodukt 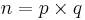
Teoremet: (a,b) = (xmod p,xmod q)
Är a och b kända samt p och q så kan x bestämmas.
[edit] 13.2.1 Garner’s Formula
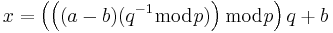
Hur ska vi använda CRT?
Kan användas för att spara beräkningskraft när vi räknar (mod n).
Addition (x + y)mod n kan representeras av (x + y)mod p,(x + y)mod q = (xmod p + ymod p),(xmod q + ymod q)
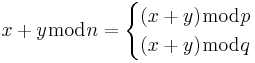
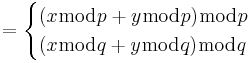
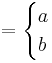
p primtal: xp − 1 = 1(mod p)
xt = 1mod n
⇒ xt = 1(mod q) och xt = 1(mod p) eftersom 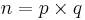
p − 1 ska vara en delare till till t och q − 1 ska vara en delare till t.
t = minsta gemensamma multipeln till (p − 1,q − 1) 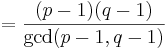
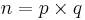
p och q stora och olika primtal.
me(mod n)
Definiera två exponenter e och d
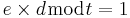
Välj en publik exponent e = till ett litet och udda tal.
d ska beräknas = inversen till emod t ⇒ 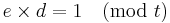
Kryptering c = memod n
Dekryptering m = cdmod n
![(m^e)^d
= m^{(e\times d)}
\left[
\begin{array}{l}
(e \times d) \bmod t = 1 \\
(e \times d) + k \times t = 1 \\
\mbox{k är ett heltal}
\end{array}
\right]](upload/images/math/7/7/7/77768485628563cd10e7154fc5fb5dad.png)
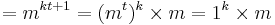 = m(mod n)
= m(mod n)
mt = 1(mod n)
mt = 1mod p mt = 1mod q
om 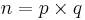
[edit] Exempel
Dekryptering och kryptering med RSA
p = 17 q = 19
Beräkna 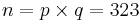 (publik)
(publik)
lcm = Least Common Multiple
Beräkna 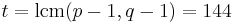 (hemlig)
(hemlig)
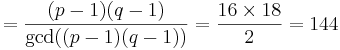
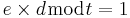
e = 5 (publik)
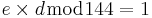
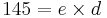 ⇒ d = 29 (hemlig)
⇒ d = 29 (hemlig)
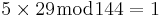
m = 201
c = memod n = 2015mod 323 = 328080401001mod 323 = 216
Dekryptering:
cd = 21629mod 323 = 50021738714629030177311081962496059484833406150976385567830453518336mod 323 = 201
[edit] 2007-12-11
[edit] RSA
Kryptering c = memod n
Dekryptering m = cdmod n = c1 / emod n
e = 17
d = 2753
n = 3233
m = 123
c = 12317mod 3233 = 337587917446653715596592958817679803mod 3233 = 855
m = 8552753mod 3233 = 123
Börja välj p och q
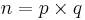
n är publik.
t = minsta gemensamma multipeln av p − 1 och q − 1.
p = 17
q = 19
p − 1 = 16
q − 1 = 18
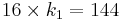
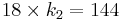
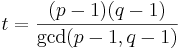
Välj e. Litet udda tal < t
e ska inte ha gemensam faktor med t då vi inte hittar ett d.
Beräkna d från 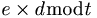
xt = 1
Fermats lilla sats
xp − 1 = 1(mod p) om p är ett primtal
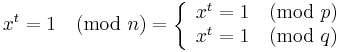
[edit] Tentauppgift kan vara
Ta fram RSA-parametrarna om p = 47 och q = 59
[edit] Svar:
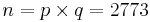
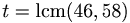
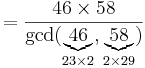
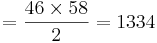
e ska inte ha gemensam faktor med t
e = 3
Kolla att 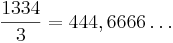
Beräkna d: 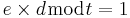
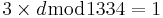 ⇒
⇒ 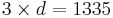 ⇒ d = 445
⇒ d = 445
Publika nycklar: n,e
Hemliga nycklar: p,q,d,t
c = memod n
m = cdmod n = c1 / emod n
(memod n)1 / emod n
Om me < n då gäller (me)1 / emod n = m
En viktig fallgrop är detta ⇒ undvik små m
[edit] Signera ett meddelande
Till exempel 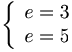
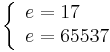
s = m1 / emod n = mdmod n
Skicka m,s
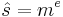
Jämför 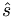 och mottaget s.
och mottaget s.
⇒ Använd två värde på e, ett för signaturen och ett för krypteringen.
Storleken på n ska vara från 2048 till 4096 bitar, samma som för Diffie-Hellman.
Kryptering: I praktiten används inte RSA för att kryptera meddelanden eftersom m < n därför används RSA för att kryptera nycklar.
[edit] 13.6
- Välj slumpmässig nyckel K + eventuell padding
- Kryptera K med RSA
- Använd ett block cipher mode för att kryptera meddelandet
- Skicka RSA-krypterad nyckel K och krypterat meddelande.
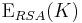 ,
, 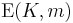 istället för att
istället för att 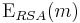
[edit] 13.4.3 Hemliga nycklar
Om man känner till en av de hemliga nycklarna (p,q,t,d) och de publika, då är det enkelt att knäcka RSA.
Två fallgropar vid signering
[edit] 1
Använd inte samma e vid kryptering och signering s = m1 / emod n
[edit] 2
Alice skickar två meddelanden som hon signerar (m1,s1) (m2,s2)
Eve konstruerar ett meddelande som uppfyller 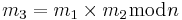
signera genom att 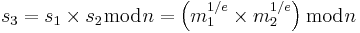
[edit] Uppgift
Ta fram RSA-parametrar om p = 11 och q = 89 välj e större än 3 och kryptera m = 68
[edit] 2007-12-17
[edit] 14 Inledning till kryptografiska protokoll
- Utbyte meddelande
- T.ex. Diffie-Hellman
[edit] A. Roller
Kom ihåg att alla kan anta olika roller, t.ex. man in the middle, DH
[edit] B. Förtroende
Inte svart-vitt
lita på någon att hantera t.ex. 10000kr.
kryptotillämpningar
minimera mängden förtroende.
- Antal människor vi behöver lita på
- Hur mycket förtroende vi behöver ge dessa människor
[edit] 14.5
[edit] C. Meddelande, steg
Specifikationerna av ett protokoll
- inte för detaljerad
- inte för enkel
- dela protokollet i flera steg
[edit] Transportlagret
- Ett givet antal bitar skall från punkt A till B. T.ex. TCP
- Ingen säker kanal, ur ett kryptoperspektiv
[edit] Protokoll och meddelandeidentifiering
- Protokollinformation
- Vilken version
- Vilket protokoll
- Meddelandenumrering
[edit] 14.5 Meddelandekryptering
Konvertera från datasymboler till bitsekvenser och kryptera.
[edit] Felhantering
- Hantera fel varsamt
- T.ex. pinkoder om 4 siffror
[edit] 15 Key negotiation protocols
- Använde nyckelutbytnadsprotokollet för att sätta upp en "session key", K
- "Session key" tenderar att vara beräkningskrävande
- Använd k för en säker och effektiv kanal
Varför använda en "session key" om vi redan har en säker nyckel?
- Om vi förlorar en ”session key” så är ändå t.ex. gårdagens information säker.
[edit] 15.2 DH + added authentication
Alice vet [p,q,g]
Väljer x från 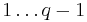
gx beräknas och skickas
Bob vet [p,q,g]
Väljer y
Beräknar gy och k = (gx)y
Skickar tillbaka gy
Alice kan nu beräkna k = (gy)x
och beräkna 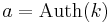
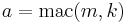
Alice skickar a och m
Bob kollar a' och jämför a = a'
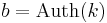
Bob skickar b och m
Alice kollar b = b'
[edit] Problem
- Samma nyckel används vid kryptering och verifiering ⇒ verifieringen ger oss inget nytt
- Inte bra att ha givna (p,q,g)
- 4 meddelande behövs, för många går att göra på 3
[edit] Verifiering: Hur ska vi välja m?
m ska vara all information som är skickad upp till nu.
Skriver Auth då menas all information som är sänt genom t.ex. en hashfunktion.
[edit] Alice
Väljer (p,q,g)
Välj x ⇒ gx
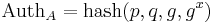
AuthA och gx skickas.
[edit] Bob
Får reda på (p,q,g)
Välj y ⇒ gy
Beräknar Auth'A, jämför med mottagna AuthA
Beräknar 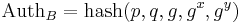
AuthB och gy skickas
[edit] Alice
Beräknar Auth'B och jämför med mottagna AuthB
[edit] Problem
Problem vid verifiering och p,q,g kan vara felaktigt valda
- Alice skickar slumptal + minsta p,Auth
- Bob väljer parametrar, beräknar gx + Auth
- Alice beräknar gy och Auth
| Alice | ↔ | Bob |
|---|---|---|
| Väljer minsta storleken på p = s | Väjer p,q,g | |
| Väljer slumptal (Nonce) på 256 bitar = Na | S,Na → | väljer x ⇒ gx |
| ← p,q,g,gx,AuthA | Beräknar AuthA(s,Na,p,q,g,gx) | |
| Kolla (p,q,g) | ||
| välj y = gy | ||
| Beräkna Auth'A och jämför. | ||
| Beräkna AuthB och k (30 bitar) | gy,AuthB→ | Kolla AuthB, beräkna k |
Ytterligare förbättring för att få k till 256 bitar ⇒ 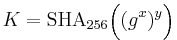
[edit] 2007-12-18
[edit] 17 The Clock
- Begränsar varaktigheten av ett dokument
- nonce
- använd klockan för att inte förväxla gamla meddelanden som nya
[edit] 18 Key Servers
Organisation som man litar på som handhar publika nycklar eller delar ut en säker nyckel samt vet vem som är vem.
- Alla användare sätter upp en publik nyckel hos "key server".
Alice, kA och Bob, kB
[edit] 18.2 Kerberos
Alice vill kommunicera med Bob.
"key server" har då kA och kB
kAB = session key
| Alice | Request “Bob” → | Key Server |
| ← EKA(KAB) | ||
| ← EKA(EKB(KAB)) | ||
| EKB(KAB) → | Bob |
- Verkar enkelt ⇒ komplicerat protokoll
- Servern måste hålla reda på alla använda kAB, session keys
[edit] 18.3 Secure Connection
Förenklad version
Förutsätter att det finns en säker kanal mellan key server och Alice samt mellan key server och Bob.
Alice vill kommunicera med Bob
key server och Alice har nyckel kA
- Alice använder ett nyckelförhandlingsprotokoll för att förhandla en session key
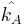
- Alice använder nu
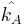 för att kommunicera med key server
för att kommunicera med key server - Bob gör som punkt 1 och för
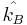
- Bob kommunicerar med key server med nyckel
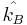
- All kommunikation via nyckelservern
[edit] 19 Public Key Infrastructure (PKI)
CA - Central Authority
CA har en egen privat och publik nyckel. Den publika publiceras. (RSA används, oftast).
"Gå med i PKI"
- Alice genererar sin publika/private nyckel.
- Alice skickar sin publika nyckel (PkA) till CA
- CA utfärdar ett Certifikat som säger att PkA
- CA publicerar PkA på sin officiella lista
- Bob samma förfarande
kommunicera Alice ↔ Bob
- Alice skickar sin publika nyckel PkA till Bob
- Bob kollar med CA om PkA är samma
- Bob skickar…
- Alice kollar…
[edit] 19.2 Universell PKI
- Omöjlig
[edit] 19.3 Multilevelcertificat
Säkerhetskedja – Bankvärlden
T.ex. Mastercard ← Firstcard →
[edit] 19.4 Bäst före-datum
- Använd inte samma nyckel en längre tid
- Behöver också certifikat bytas